Usage: Choquet Integral
This page shows the usage of Chouet Integral Calculation Site.
This software caclate the Choquet integral by CGI.
The purpose of this site is to understand Choquet Integral.
If you calculate Choquet Integral a lots of times, I recommend to use Fuzzy Integrals(Multipurpose).
Functions
- To input fuzzy measure values
- To check the monotonicity of the fuzzy measure
- To calculate Coquet Integral
- To show the calculation process by a table
- To show the calculation process by a figure
Example
This document explains the usage using the following example :
There are 3 workers, Mike, Kate and Nancy.
Mike can produce products 3kg per hour; Kate can produce 4kg; and Nancy can produce 5kg. If Mike and Kate work cooperatively, they can produce 8kg per hour.
If Mike and Nancy work with cooperatively, they can 9kg per hour.
If Kate and Nancy work cooperatively, they can produce 10kg per hour.
If the 3 persons work cooperatively, they can produce 15kg per hour.
One day, Mike works 10 hours; Kate works 8 hours; and Nancy works 5 hours.
They start to work at the same time.
How much product (output) can be produced?
We calculate the output using Choquet integral model.
Input: number of evaluation items
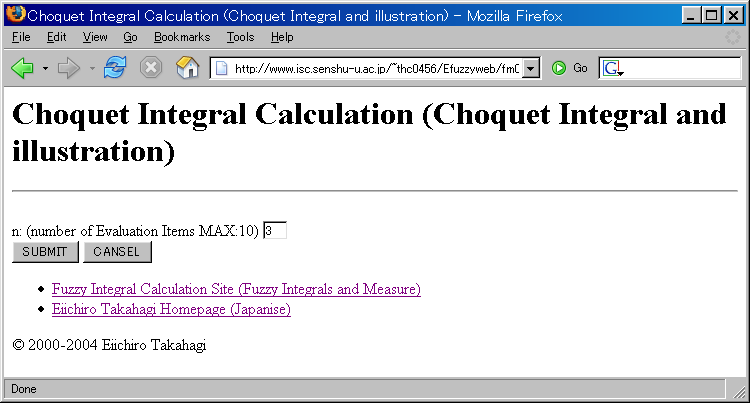
- n:(number of evaluation items Max10)
- In this example, evaluation items are workers, so the value is number of workers, 3.
Input: fuzzy measure values, input values and evaluation items' names
Fuzzy Measure Values
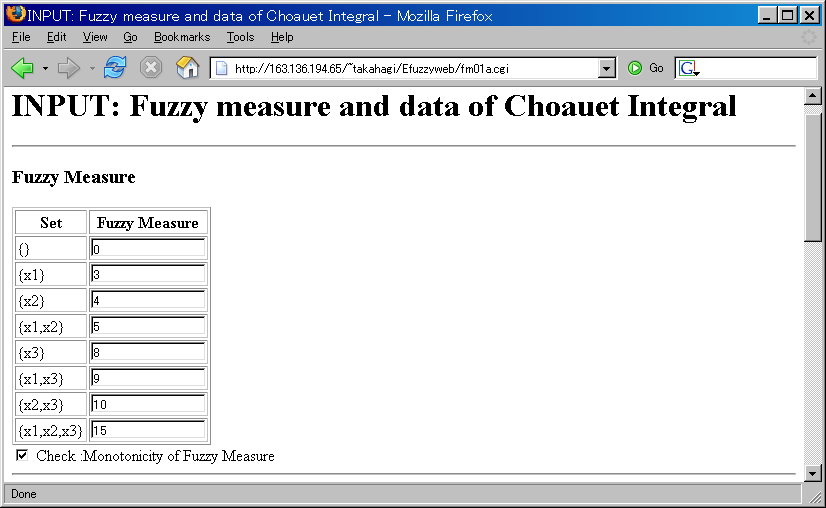
- Check: monotonicity of fuzzy measure (Check Box)
-
- If you check the box, the system check the monotonicity of fuzzy measure.
If you use (ordinal) monotonicity fuzzy measure, I recommend to check the box.
If the box is not checked, the system can not display the illustration of the calculation process.
- Fuzzy Measure Values
-
Example: x1: Mike, x2: Kate, x3: Nancy
-
You must set g{}= 0
Input Values
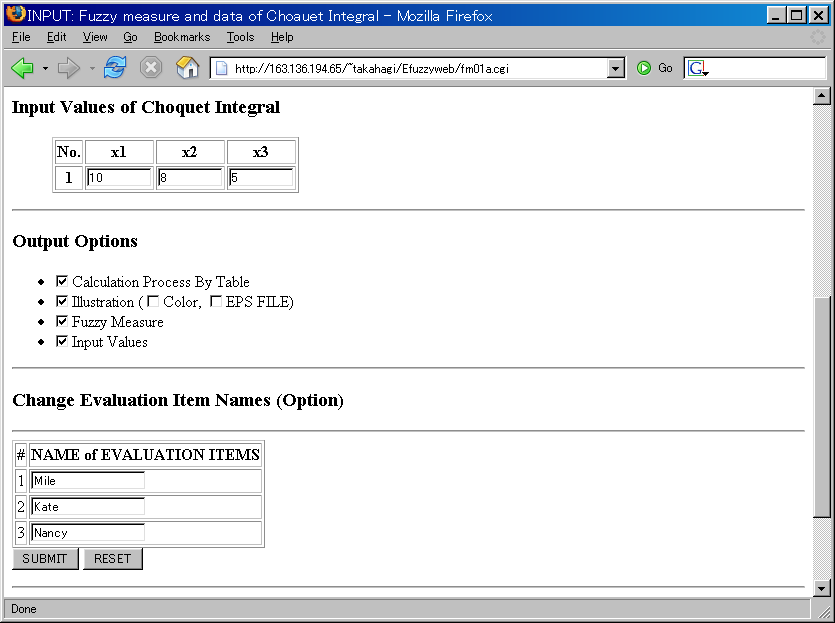 Input Values
Input the input values of Choquet integral.
Input Values
Input the input values of Choquet integral.
Example: x1(Mike):10, x2(Kate):8, x3(Nancy):5
Options
Check the output items which you need.
Evaluation Items (Option)
Change the evaluation items' name, if you need.
Example: x1 -> Mike, x2 -> Kate, x3 -> Nancy
Output of Choquet Integral
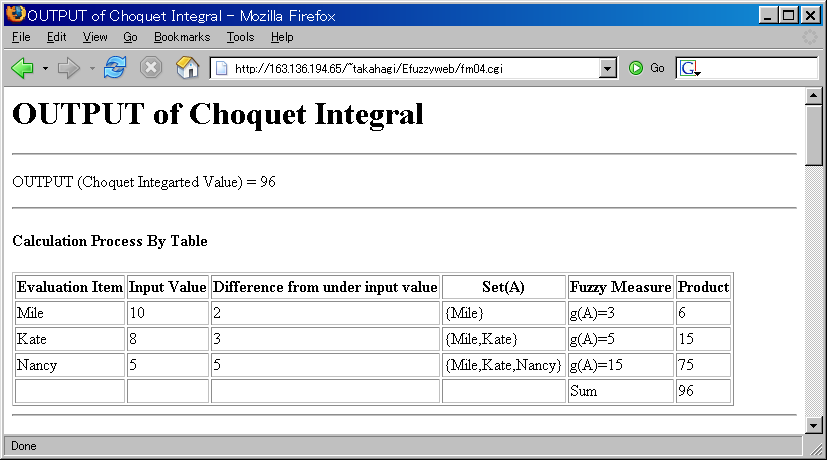
Output (Choquet Integrated Value)
Output value of Choquet integral
Example: The output 105kg shows the product amount of the day.
Calculation Process by Table
This table shows Calculation Process of Choquet Integral.
Example:
- Sorting
- Evaluation items are sorted in descending order of input values
- Deference from under input value
- Bottom Line: Deference from 0
Ex.) Mike's Deference from under input value = h(Mike) - h(Kate).
- Set (A)
- Set is the accumulation of the evaluation items.
- Product
- (Deference from under input value) * g(A)
- Output
- Sum of product values
Illustration
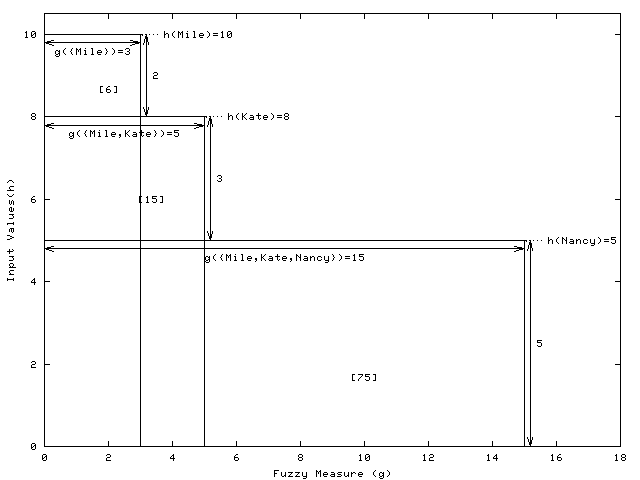
- 0 to 5(h(Nancy))
- 3 persons (Mike, Kate and Nancy) are working, so we use the fuzzy measure g({Mike, Kate, Nancy})=15. Therefore, from 0 to 5, g({Mike, Kate, Nancy}) * ( h(Nancy) - 0 ) = 75.
This calculation is correspond to Nancy's line of the calculation table.
- 5 (h(Nancy)) to 8(h(Kate))
- Mike and Kate are working, so we use the fuzzy measure g({Mike, Kate})=8. Therefore, from 5 to 8, g({Mike, Kate}) * ( h(Kate) - h(Nancy) ) = 24.
This calculation is correspond to Kate's line of the calculation table.
- 8(h(Kate)) to 10(h(Mike))
- Only Mike is working, so we use the fuzzy measure g({Mike})=3. Therefore, from 8 to 10, g({Mike}) * ( h(Mike) - h(Kate) ) = 6.
This calculation is correspond to Mike's line of the calculation table.
- Sum of all Areas
- The output of the day is sum of 3 areas, 75+24+6=105
© 2005 Eiichiro Takahagi




