[視力検査]
視力検査で使われる"C"の形をした、円周の一部が欠けた円
(Landolt Cと呼ばれる)を考えよう。
視力の良い人は欠けた部分がちゃんと見えるが、視力の悪い人は欠けた部分が見えず、
ただの円に見えてしまう。つまり、目の悪い人は欠けた部分がふさがって見えるのである。
これは本来離れているべき二点が、眼球レンズのなんらかの問題により「一点」として
見えるため、「二点がくっついてしまった」のである。

もちろん、どんなに目の良い人でも、欠けた部分の隙間をどんどん 狭く小さくしていけば、最終的には隙間がくっついているように見える状況が訪れる (視力が2.0の人でも、視力3.0に相当するLandolt Cマークをちゃんと見ることはできない)。 「隙間があるのに、隙間がないように見える」という状況は誰の目にも 遅かれ早かれやってくると言える。
[テレビ画面の解像度]
似たよう状況は、テレビ画面やコンピュータの画面にも見受けられる。
(ただし、この場合は隙間が見えなくなる方を期待しているので、
ある意味、視力検査とは「逆」の状況かもしれないが。)
遠くから画面を眺めていると滑らかな画像が見える。ところが、画面に目を近づけると、
無数の小さな点(ドット)が見えてくる(水滴などを垂らすとより効果的である)。
滑らかな画像だと思っていたものは、小さなな点の集まりだったというわけだ。
つまり、遠くから見ることによって、ドットとドットの間の隙間が「潰れて」見えなくなり、
滑らかな画像のように見えていただけだったのだ。
これらの状況を簡単にまとめると、「二点が一点にしかみえない」と 言い換えることができるだろう。 本来2つあるべきものが、1つしか見えないということだ。 すなわち、「遠すぎて見えない」という状況は、「遠すぎるため、二点が一点に潰れて見える」 時に生じるのである。この問題は、テレビや映写プロジェクター、 デジタルカメラなどの電気製品で「解像度」と呼ばれている性質と関連している。
[土星の環]
天体観測において、あまりに遠くにある天体は、その詳細がよく見えず、二点が一点に潰れて
しまうことがよく起きる。この問題が最初に起きたのは「土星の環」の観測である。
(公式に認められた)人類史上最初の望遠鏡による天体観測は、1610年前後にガリレオが 行った観測である。その成果は「星界の報告」という著書によって発表され、ルネッサンスの 文化人に大きな衝撃を与えた。この本で取り上げられているのは、地球照、月面、天の川、そして 木星の衛星(現在、ガリレオ衛星と呼ばれる4つの衛星、イオ、エウロバ、ガニメデ、カリスト) の発見とその運動の様子である。この後も、太陽黒点、金星の満ち欠けなどに関する観測が 論文や書簡集として出版されている。
しかし、ガリレオは土星と土星の環についても観測を行っていたのである。 ところが、ガリレオが用いた望遠鏡の「解像度」は低く、 土星の環の形を詳細に捉えることができなかった。 すなわち二点が一点に潰れてみえていたのである。 土星の「不思議な形」に当惑したガリレオは、友人への手紙(Letter to Belisario Vinta, 1610) にその不思議さを伝えてはいるが、公の形で発表することができなかった。 (この手紙の中で、ガリレオは土星の環を「耳」と表現し、 またその形は年によって変わることにも気づいている。)

上の図の左は、1610年の手紙の原文(Letter to Belisario Vinta)。 右は、手紙の内容を、1613年に "Istoria e dimostrazioni intorno alle macchie solari" として出版したもの。英訳すると"Stroy and demonstrations around solar stains"。 原著全文のコピーは Internet archiveで入手可能。
ガリレオ博物館(Museo Galileo)の資料にあるように、解像度の悪い望遠鏡で 土星の環を観測すると、いろいろな形に見えるため、観測者は非常に困惑する。 この問題を解決したのが、オランダのホイヘンスである。ホイヘンスは1659年その著書 "Systema Saturnium"において、 土星には環があり、その傾きが30年周期で変化することを 明らかにした。年々変わりゆく環の形を、解像度の悪い望遠鏡で観測していたために、 土星は「変幻自在の不思議な形」をしていたように見えたのである。
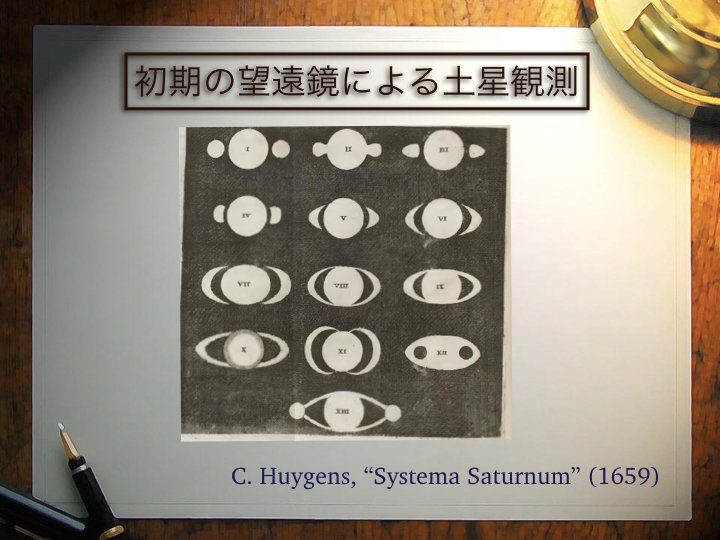
上の図は、ホイヘンスの著書においてまとめられた「今までに報告された土星の形」である。 「猿の耳」から「豚の鼻」まで、様々な形が報告されているが、これらは「年々傾きが変わりゆく 土星の環を、性能の悪い望遠鏡で観測した結果」であることを強調している。
現在amazon.co.jpなどで安価で手に入り、 ガリレオの望遠鏡よりちょっとだけ性能がよい望遠鏡として、 VixenのA80Mfという屈折望遠鏡がある。これを用いた 私自身による観測結果と比べて見ると、 「二点が一点に見える」問題によって、どの段階の土星の形がどのように歪曲した観測となったか 確認し、納得することができるだろう。
さらなる問題は、土星の環そのものの構造にも見られる。1675年にカッシーニは 土星の環に隙間があることを発見した。現在、 「カッシーニの間隙」 と呼ばれる構造である。下の図は、NASAのハッブル宇宙望遠鏡が撮影した土星の環であり、 その最大の隙間がカッシーニの間隙である。

この隙間は、私の観測写真(下図参照)にも写っていないし、
ガリレオのスケッチにも当然描かれていない。
すなわち、視力検査同様、カッシーニのそれに比べて望遠鏡の性能が悪く、
二点が一点に潰れてしまったため、隙間が隙間として見えなかったのである。

「二点が一点に潰れる」問題は、解像度の問題として捉えることができる。 これは数学的に考えるのがもっとも適切である。 天体の大きさを\(x\), 天体と地球の間の距離を\(y\)としたとき、 天体を見込む角度\(\theta\)は正接を用いて\(\tan\theta = \frac{x}{y}\)と 表すことができる。\(y\gg x\)のとき、すなわち\(|\theta| \ll 1\)の場合、 テイラー展開を用いると\(\tan\theta \sim \theta\)と近似できるので \[ \theta \simeq \frac{x}{y} \] と表せる。\(\theta\)が小さいだろうことは容易に推測できるが、それがどんなに小さくても (0でなく)「有限な値」であれば、天体を見込む角度が(観測者には)認識できることになる。 したがって、遠方\(y\)にある、距離\(x\)だけ 離れた二点は二点として観測することができる。 ところが、\(x\)に対して\(y\)が非常に大きい時、すなわち有限の\(x\)に対して \(y\rightarrow\infty\)という極限を考えると\(\theta \rightarrow 0\)となってしまう。 これは「平行光線」と見なされる。遠方の点光源から到来する光は平行光線として認識されるので、 このような状況で「二点は一点に」潰れてしまう。すなわち、望遠鏡の性能における 分解能の限界以下に\(\theta\)の値が落ち込んだとき、\(\theta=0\)と見なされ、 観測者は詳細な構造を見ることができなくなるのである。