手順は以下の通りです。
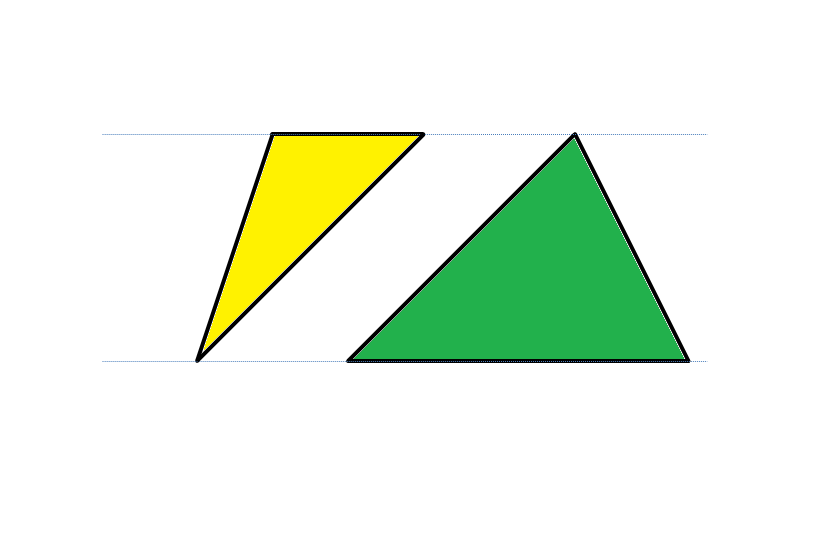
手順1 2つの三角形の面積を求める。
手順2 2つの三角形の面積を足して台形の面積を求める。
台形の面積を返す関数の作成に先立ち、あらかじめ三角形の面積を返す関数を作っておきます。この三角形の面積を返す関数を呼び出して、台形の面積を返す関数で三角形の面積を求めます。
Function 〜 End Functionの間には何行かいてもかまいません。それぞれの行が、文法上正しく記載されていれば何行でも使うことができます。またプログラムは上の行から下の行に向かって処理されていきます。 ここでは、複数行を使って一連の計算をすることを説明することを意図しています。少々無理やり手順を分けていますが、複数行を使って計算することを意図していることをご理解いただけますようお願いいたします。
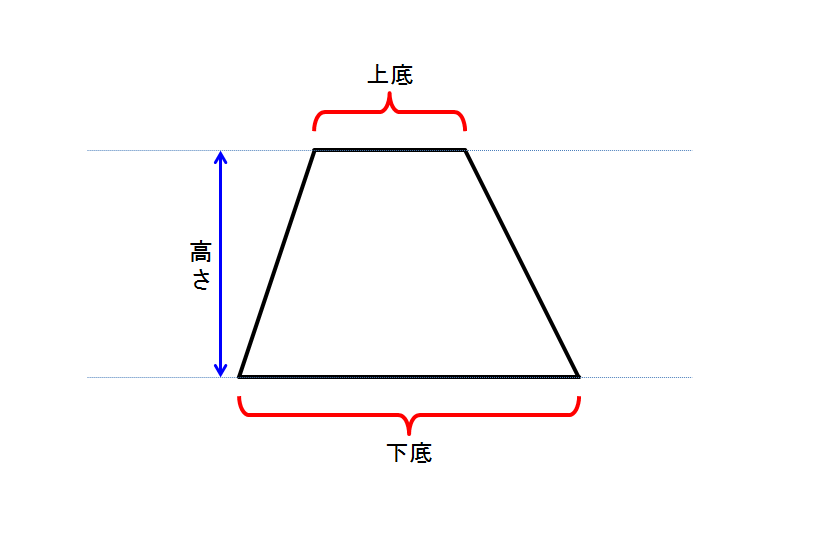
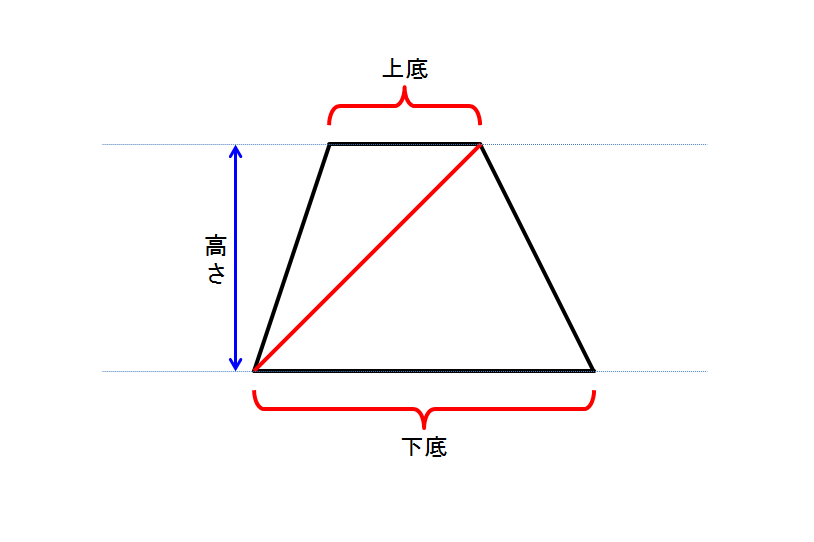
公式をつかわずに台形の面積を求めることを考えます。台形に対角線を引くことにより、2つの三角形の和が台形になることを利用します。



手順は以下の通りです。
手順1 2つの三角形の面積を求める。
手順2 2つの三角形の面積を足して台形の面積を求める。
台形の面積を返す関数の作成に先立ち、あらかじめ三角形の面積を返す関数を作っておきます。この三角形の面積を返す関数を呼び出して、台形の面積を返す関数で三角形の面積を求めます。
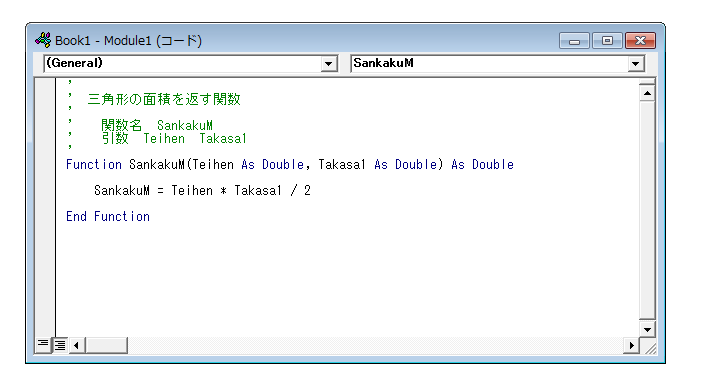
三角形の面積を使って台形の面積を求めてみます。そこで事前の準備として、三角形の面積を求める関数を作っておきます。
関数名は SankakuM
引数は Teihen と Takasa1 です。
データの型は倍精度浮動小数点型です。
引数の「Takasa1」は台形の面積を求める関数で「Takasa」を使いたいので、それと明示的に分けるために数字を追加しています。また、アルファベットと数字を組み合わせた変数名(関数名・引数の名前など)を使用することができることの説明でもあります。
計算方法としては、三角形の面積の公式を使います。
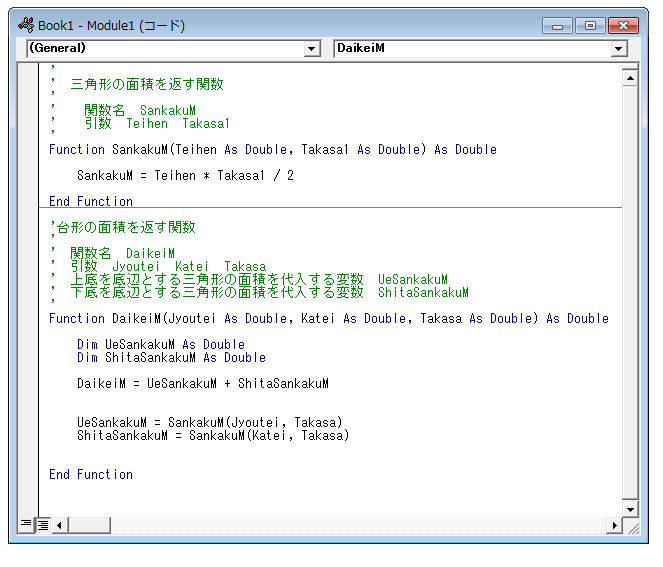
三角形の面積を返す関数の下に続けて台形の面積を返す関数を作ります。
関数名は DaikeiM
引数は Jyoutei Katei Takasa
そして、「Jyoutei」を底辺とし、「Takasa」を高さとする三角形の面積を代入する変数を「UeSankakuM」とします。
同様に、「katei」を底辺とし、「Takasa」を高さとする三角形の面積を代入する変数を「ShitaSankakuM」とします。
変数はすべて倍精度浮動小数点(Double)とします。
今までと同様に fanction 行を記述します。
Function DaikeiM(Jyoutei As Double, Katei As Double) As Double
と入力し改行するとend function行が追加されます。
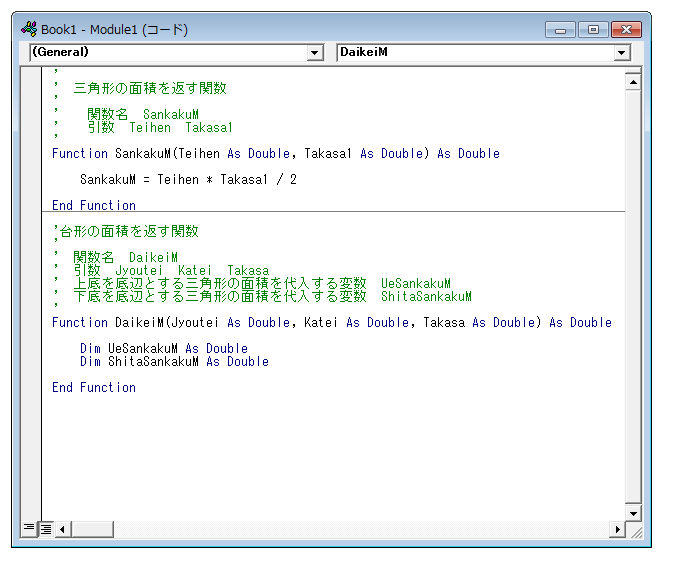
Function行とEnd Function行の間に、UeSankakuMとShitaSankakuMの宣言を行います。
dim UeSankakuM as double
dim ShitaSankakuM as double
と入力します。これで関数名・引数・変数の準備ができました。
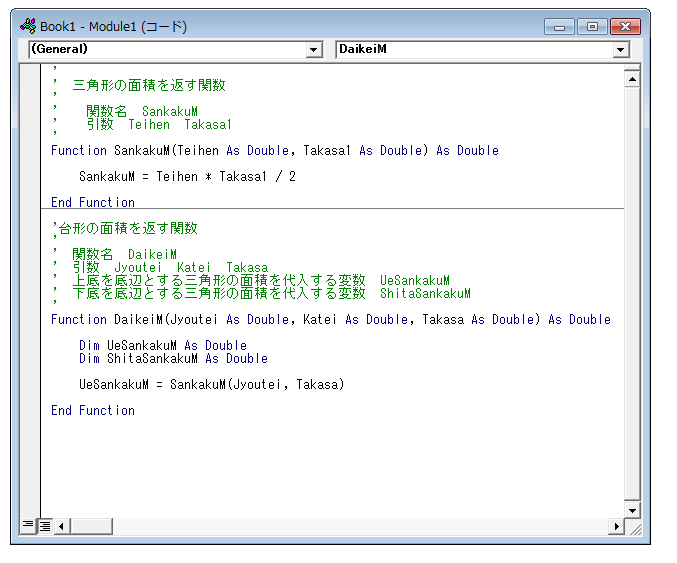
次にUeSankakuM に先ほど作った三角形の面積を返す関数「SankakuM」を使って上底を底辺とする三角形の面積を代入します。
uesankakum = sankakum(jyoutei, takasa)
と入力します。改行すると一部の文字が大文字に変わります。
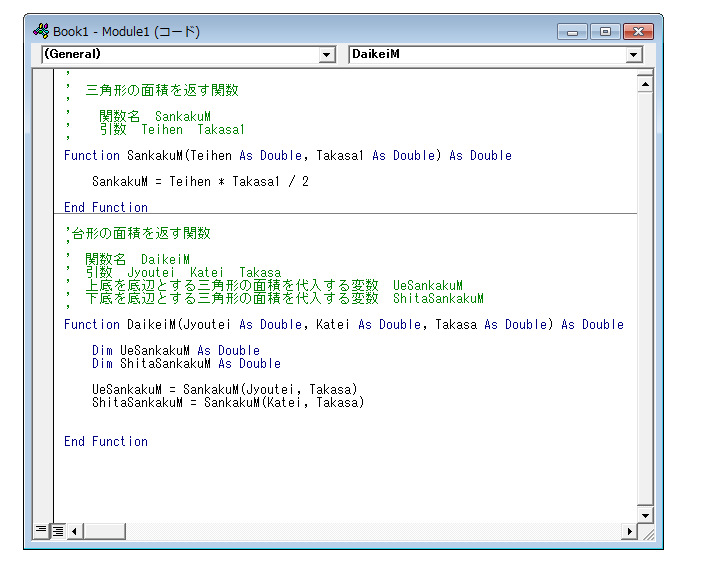
同様にShitaSankakuM に「SankakuM」を使って下底を底辺とする三角形の面積を代入します。
shitasankakum = sankakum(katei, takasa)
と入力します。この時点で2つの三角形の面積を求めることができました。
最後に、2の三角形の面積を加えて、台形の面積を求めます。
daikeim = uesankakum + shitasankakum
と入力します。
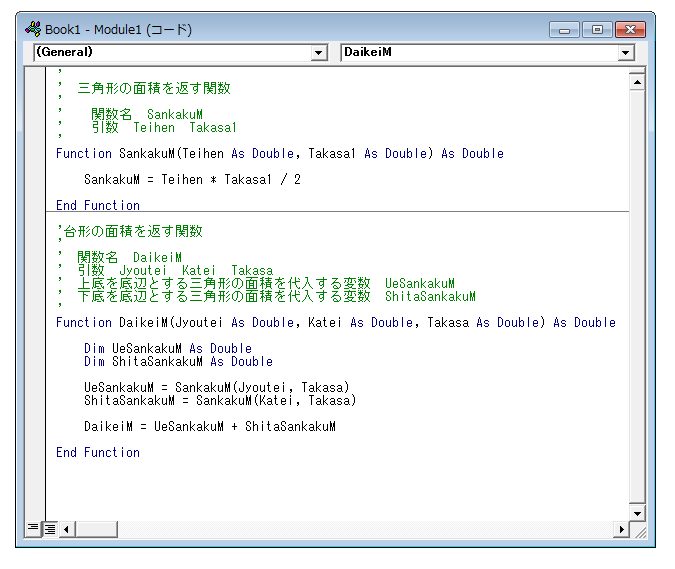
プログラムは上から下に向かって実行されます.
今回の例では、「UeSankakuM」を求めた後に「ShitaSankakuM」を求めていますが、これはどちらを先に行っても結果には影響がありません。
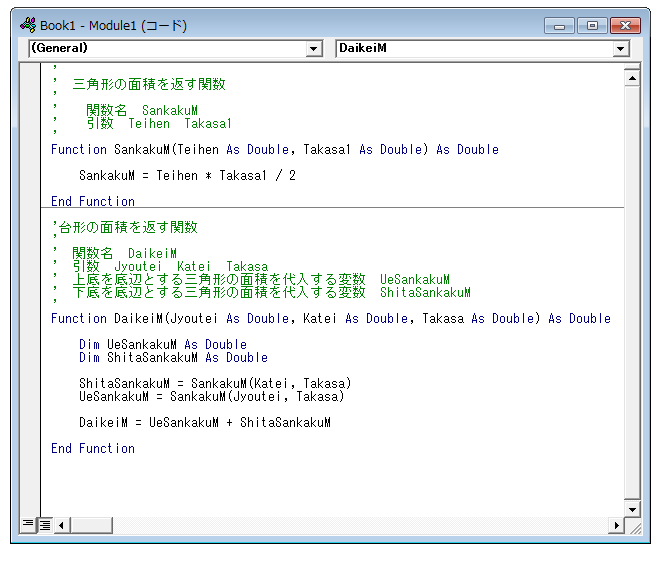
2つの三角形の面積を求めた後に、「UeSankakuM」と「ShitaSankakuM」を足して「DaikeiM」を求めていますが、この行は、2つの三角形の面積を求めた後でなければ台形の面積を求めることができません。
以下の例では、計算結果hは「0」となってしまいます。