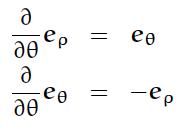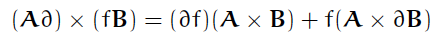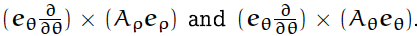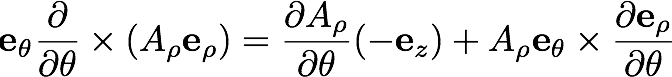電磁気学A(東京大学前期課程)の講義情報
2017年度Aセメスター(木曜日2限)開講:理科II,III類(4,22,24組)
このページの目次
- 教科書/参考書
- はじめに
- [第1回] 電磁気学と電気力学 [Sep.27]
- [第2回] 力学的電磁気学:クーロン力 [Oct. 11]
- [第3回] クーロン力の導出(続き)、∇xE=0の意味 [Oct. 18]
- [第4回] ガウスの法則の応用、静磁場、∇・B=0の意味 [Oct. 25]
- [第5回] 静電場に対するガウスの法則の応用などの復習 [Nov. 1]
- [第6回] クーロンの法則からガウスの法則へ:極座標の微分演算子[Nov.15]
駒場で電磁気を担当して3年目となる。1年目のテーマは、力の近接作用の理解を目標とした。
「場」という概念はファラデーが19世紀に提案したもので、電磁気学の現象が遠隔作用で
生じるとはとうてい考えられない、という彼の卓抜した物理センスによって編み出されたも
のだ。(実は、ニュートンも遠隔作用については否定的な考えをもっていたようだが、
近接作用による重力理論の定式化には成功しなかった。)
近接作用こそが力の伝播を記述する正しい物理である、という
考えは現代物理においてもその本質にかかわる重要な考え方だろう。
2年目はクーロン力とアンペール力(グラスマン力)の比較を通し、電荷と電流の
役割の相違についての理解を目指した。1年目の経験(および自分自身の実感)から、
「電磁気学の初学者がつまずきやすいのがどうも磁気現象らしい」という感覚をもった。
たしかに近接作用の考え方が比較的わかりやすかった静電場に対し、
「(磁場生成に対する)電流の役割」ついての説明が不足がちな点や、
一見して込み入った感じに見える外積による磁場の記述(ビオサバールの法則など)などにより、
静磁気の理論を「煙に巻かれた、曖昧な感じのするもの」と感じる人は多いだろう。
特に、歴史的には葬り去られた「電流素片」の概念に着目し、
その考え方の良い点/悪い点をを通して、静磁気現象について議論した。
3年目の今年は、「電磁気学」ではなく「電気力学」
として電磁気の現象を理解することを目標にしたい。「電磁気学」と題された
日本の教科書が多いのに対し、「電気力学」すなわちElectrodynamicsと題された教科書が
アメリカには多い。これはなぜだろうか?「場」という「マクロな物理体」ではなく、
電子などの電荷をもつ質点に対するローレンツ力によるミクロな物理体から
講義を始め、電荷と電流の関係を明らかにしつつ、マクスウェル方程式へと
話を進めていく。
電磁気学 ... Electromagnetism: 日本の教科書に多い。
電気力学 ... Electrodynamics: アメリカの教科書に多い。
朝永、シュインガー、ファインマンが完成させたのが、Quantum Electrodynamics、略して
QED.
Maxwellの書いた本は「電気と磁気に関する理論」, "A treatise on electricity and magnetism" (1873)
[原著(pdf)]
Maxwell方程式を現在のような形に書き直したHeavysideの全ての著作には
"Electromagnetic"という言葉が入っている。例えば、"Electromagnetic Theory" (1893)
[pdf]など。
こうして見ると、日本の教科書は、英国における初期の電磁気学研究に忠実に基づいて
構成された「古い/伝統的なやり方」であり、
アメリカの教科書はそこから脱却した「新しい/革新的やり方」であることが察せられる。
Maxwellの理論が最初に登場した時には、まだ電子の発見がなされていなかったことを考えると、
オリジナルの「電磁気学」にはミクロの観点があまり強く表されていなかったではないか?(マクスウェルの著作をまだ読んでいないので断定はできない。ただ、中身を覗くと、ベクトル解析の
解説の後、静電気から理論が始まっている。これは日本の教科書とほぼ同じ構成である。)
電流のミクロな理解はDrude理論(1900)に祖があると考えるより、
1837年のファラデーの予想に
基礎があると考えるべきだろう[Ot00]。ファラデーの予想を確かめようとしてローランドの実験
が1876年に行われ、それを元にして電流の正体である「電荷の運動」に興味が集まった。
1881年にJ.J.Tomsonがv×Bの形を思いつき(ただし係数が誤っていた),
1889年にO. Heavysideが係数を正し、最後に1892年にH. Lorentzが電場からの寄与も含めて
F = qE + qv×B
とまとめて書いたとき、電流の微視的な解釈はほぼ定着したのであろう(これをローレンツの力
と呼ぶのはヘビサイドやトムソンに申し訳ないような気もするが)。
1897年にJ.J.Thomsonが電子を発見したのは、この確信の下に成し遂げられたもの推察する。
J.D.JacksonのClassical Electrodynamicsも、Feynmanの教科書も、このローレンツの力より
「電気力学」の議論を始める。
磁石や電流よりも、「動く電荷」の方が基本的である、という考え方である。
(あるいは、微小電流をj = qvと表せば、ローレンツの力は
F = qE + j×Bとなり、試験電荷/試験電流と
電場/磁場の関係が明確となる。)
∇の説明(デカルト座標)。∇を使ったMaxwell方程式は
∇・E = ρ/ε0.
∇×E + ∂B/∂t= 0.
∇・B = 0.
∇×B -ε0μ0∂E/∂t=
μ0j
だが、成分で書くともう少し馴染みのある形になる。実際の数値計算を行う際も成分で
書き下した方がやりやすい。その一方で、表式が長くなるため、論文にしたり、
理論計算するときは面倒になる。状況に応じて使い分けるべき。
場の概念に慣れる必要がある。が、電磁場では次の2種類だけをよく理解しておくだけで
(ほぼ)十分。(i) 放射型の場(rに比例するような場)(ii)渦型の場(rに
直交するようなもの)。それぞれのタイプのdivergence(発散)とcurl(循環)を計算すると
特徴的な値となる。
時間依存性をなくしたMaxwell方程式は、静電場と静磁場の2つに分離(decouple)し、
前者が(i)型、後者が(ii)型の場となる。(これはどういうことか、調べてみよ。)
高校の物理では、重力との類似性を強調したクーロン力の表式を採用したが、
大学の電磁気学では「場」の概念を強調した表式を採用する。ポイントは
2つの電荷q1とq2を、試験電荷と源電荷に分類して考える点で、
後者が電場を作る「源電荷」と見なされ、前者は置かれた場所にある場を感じ人間にその存在を
力という形で教えてくれる「試験電荷」と見なされる。(作用反作用の法則により、どちらを
どちらの電荷とみなすかは相対的にしてよい。だが、その物理的解釈は首尾一貫させる必要
がある。)
一方、「磁力」に関しては、高校では(クーロン力に相当するような)定量的な議論は行わず、
磁力の公式のようなものは習わなかった。しかし、小学校では、電池と豆電球からなる
簡単な電気回路と共に、棒磁石の実験/実習を用いた電磁気学の学習を経験したはずである。
なぜ、電気の方は続く学習過程では詳細に扱っていくのに、
磁気のほうは簡単な実験や直感的な説明のみで止めてしまうのであろうか?2つの電荷の間に働く力
がクーロン力だとすると、磁気の現象に関しても「磁力」とは2つの磁極の間に働く力だろう、と
ナイーブに考えるだろう。そうだとすれば、クーロン力のような逆二乗則に従うような中心力が
期待されるはずだ(実際、アンペールはこの先入観から抜け出せなかった)。
しかし、そのような力は高校の物理では登場しない。
2つの棒磁石の間に働く力に関しては、定性的な研究を小学校の理科で行うのみだ。
実験をとおして、N極同士、あるいはS極同士では反発し、異なる磁極では引き合う、
ということは学ぶ。(また、磁力線のスケッチや、砂鉄を用いた実験などはやる。)
しかし、その大きさに関する定量的な説明は一切行われない。
電荷は「電気単極子」であり、棒磁石は「磁気双極子」であるというのが、電気と磁気を
分けるおおきなポイントで、両者の違いを初学者に説明するのは若干骨が折れる
(ましてや小学生には)。しかも、双極子であるNS磁石は単極に分離することができない。
(なぜか?という問いは物性物理で習うであろう。)磁気現象でクーロン力のような
簡明な公式/法則が見つからないのは、「双極子から始まる」磁気現象の特徴のせいでもある。
また、ローレンツ力で見られるように、磁力が中心力ではないのも、重力に慣れ親しんだ者には、
違和感がある。
マクスウェル方程式を、静的な場の場合に適用すると、時間微分が消えて、
電場(静電場)と磁場(静磁場)は分離(decopule)し、
前者が放射型、後者が渦型のベクトル場に対応していることが明らかとなる。
静電場を記述する2つの微分方程式のひとつを積分すると、クーロンの法則が
得られる。ただし、「積分」といっても「三重積分」(体積積分)である。
体積積分に不慣れな人が多いため、球の体積を体積積分で計算する例題を解いてみた。
三重積分と累次積分との関連性などを議論し、残りは実際の計算(積分計算)に費やした。
まずはデカルト座標でやってみた。∫dy(a
2-z
2-y
2)
1/2の計算で手が止まる人が少しいたので、この累次積分では(偏微分のように)
zを定数のように扱ってよいことを、追加説明した。
「Jacobian(ヤコビアン)の計算で、デカルト座標から3次元極座標への変換の際、θとφの
位置を変えた時、符号が変わるのではないか?」という質問がありました。
行列式の特徴で、列同士の交換操作に対して、行列式はたしかに反対称です。
符号の問題に関しては、体積は常に正値となるべき量ですから、
多重積分で登場するヤコビアンは絶対値記号を込みにして定義する必要がありました。
が、講義ではそうしておりませんでした。ここで修正します。
まずは3次元空間における変数変換(x,y,z)→(r,θ,φ)に対するヤコビアンは、
それぞれの座標系における体積要素を等しくするための因子として定義されます。
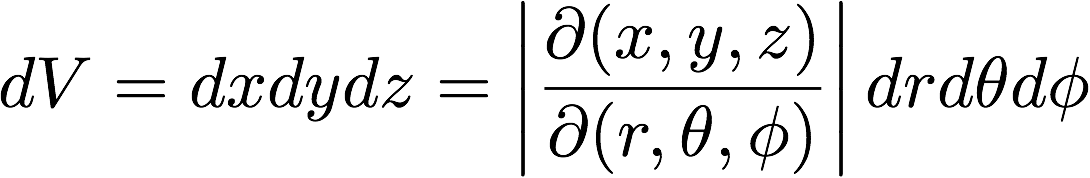
ヤコビアンは行列式の形となり、この場合(3次元)次のような形式となります。
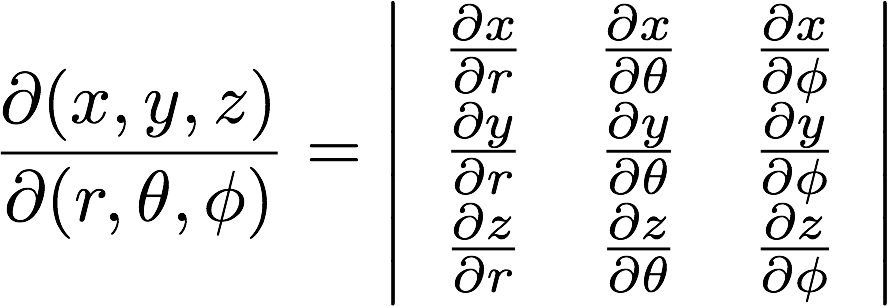
上の行列式で、2列目と3列目を交換すると、符号が反転します。すなわち
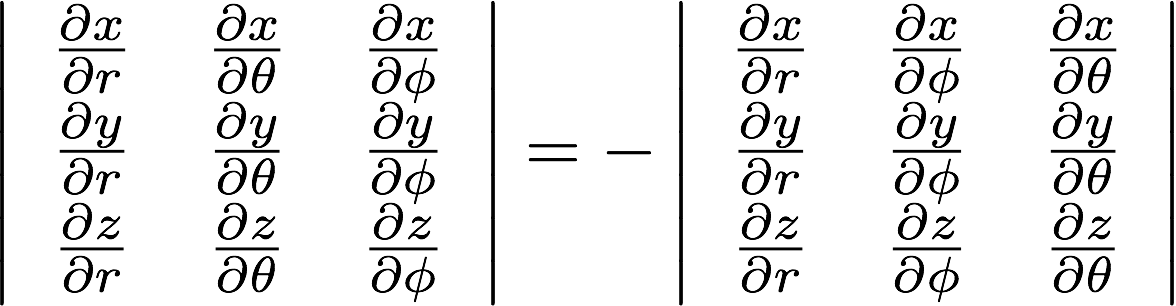
左辺の行列式は計算するとr
2sinθ、
右辺の行列式は-r
2sinθとなります。
この一方で、θとφの順番は任意だから、最初の式において、θとφの位置を交換した表現
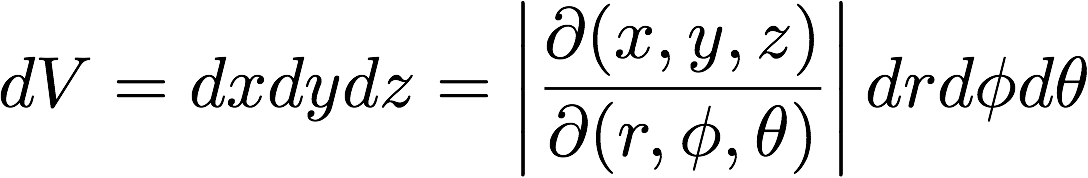
を採用しても等価なはずです。しかし、絶対値がないと、
この場合のヤコビアンは(上で計算したように)
-r
2sinθとなって、符号がずれてしまいます。ヤコビアンの絶対値を使用すると
この問題は回避されます。おなじように、xとy、rとθなど、任意の2つの変数の位置を
交換することで生じる符号の問題も、絶対値を採用することで回避されます。
(1) ガウスの法則を使って、線電荷のつくる静電場を求めること
(2)クーロンの法則とマクスウェル方程式の線型性を利用して線電荷のつくる静電場を求めること。
結果:
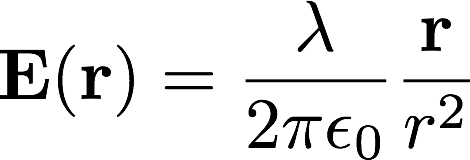
注意点:対称性(特に軸対称性)に着目しつつ、静電場の条件を絞っていく。
静磁場の方程式の分析:
ガウスの法則の積分バージョンの応用について:球状の一様電荷体の場合への適用
(レポート[10点])。
目的:クーロンの法則がガウスの法則を満たしていることを示すこと。
2つの方法で示せる:(1)デカルト座標を用いた方法 (2)極座標を用いた方法。
講義中のリクエストで、後者を選択。まずはガウスの法則の右辺∇・E
を計算するために極座標への座標変換を計算する。
全微分-偏微分の計算の練習も兼ねて、\(d(r^2)=d(x^2+y^2+z^2)\)の計算を行う。この結果を利用して∂/∂xを極座標で書き直す。
やり残した計算はレポートとする。微分演算子の書き換えのみは10点、ベクトル場の書き換えも含んだ完全版の計算は20点。
[解説]
動径の2乗の微分は\(2rdr = 2xdx + 2ydy + 2zdz\)となるので、整理して\(\displaystyle dr = \frac{x}{r}dx + \frac{y}{r}dy + \frac{z}{r}dz \)を得る。これは3変数関数\(r=r(x,y,z)\)の全微分\(\displaystyle dr=\frac{\partial r}{\partial x}dx +\frac{\partial r}{\partial y}dy +\frac{\partial r}{\partial z}dz \)と同じだから, \[ \frac{\partial r}{\partial x} = \cos\phi\sin\theta, \quad
\frac{\partial r}{\partial y} = \sin\phi\sin\theta, \quad
\frac{\partial r}{\partial z} = \cos\theta\]という関係式が手に入る。
以上の結果をまとめると\[ dr = \mathbf{e}_r\cdot d\mathbf{r}\]と簡潔に表すこともできる。
ただし、\(\mathbf{e}_r\)は動径方向の基底ベクトルであり、\(d\mathbf{r} =(dx, dy, dz)\)である。
同様の計算を行うと\(d\theta, d\phi\)についての関係式も得ることができる。まとめると
\[ dr = \mathbf{e}_r\cdot d\mathbf{r}, \quad d\theta = \frac{1}{r}\mathbf{e}_\theta\cdot d\mathbf{r}, \quad d\phi = \frac{1}{r\sin\theta}\mathbf{e}_\phi\cdot d\mathbf{r}\]となる。
偏微分の計算を必要な時に毎回行うのはとても面倒なので、一度手を動かして納得したら、上の関係式を覚えてしまうとよい。個人的な経験ではあるが、後々色々な計算をするときに非常に助かる(例えば、量子力学における角運動量の理論など)。ただし、極座標系の基底\((\mathbf{e}_r,\mathbf{e}_\theta,\mathbf{e}_\phi)\)とデカルト座標系\((\mathbf{e}_x,\mathbf{e}_y,\mathbf{e}_z)\)の間の線形関係式も記憶しておく必要がある。
\[
\mathbf{e}_r = \cos\phi\sin\theta\mathbf{e}_x + \sin\phi\sin\theta\mathbf{e}_y +
\cos\theta\mathbf{e}_z, \\
\mathbf{e}_\theta = \cos\phi\cos\theta\mathbf{e}_x + \sin\phi\cos\theta\mathbf{e}_y -
\sin\theta\mathbf{e}_z, \\
\mathbf{e}_\phi = -\sin\phi\mathbf{e}_x + \cos\phi\mathbf{e}_y.
\]
これを行列を使って表すと
\[
\left(\begin{array}{c} \mathbf{e}_r \\ \mathbf{e}_\theta \\ \mathbf{e}_\phi\end{array}\right)
=
R(\theta,\phi)
\left(\begin{array}{c} \mathbf{e}_x \\ \mathbf{e}_y \\ \mathbf{e}_z\end{array}\right)
\]
と書ける(上の式により、\(R(\theta,\phi)\)の具体的な表記は自明なので省略)。
\(R=R(\theta,\phi)\)は、\(R^TR=RR^T=I\)という関係式を満たすので3次元の直交行列である。
したがって\(R^{-1}=R^T\)でもある。
偏微分の計算が終わったので、次に微分演算の変数変換について計算することができる。
たとえば、\(\displaystyle \frac{\partial}{\partial x} = \frac{\partial r}{\partial x} \frac{\partial}{\partial r}+ \frac{\partial\theta}{\partial x} \frac{\partial}{\partial \theta} + \frac{\partial\phi}{\partial x} \frac{\partial}{\partial \phi} =
\cos\phi\sin\theta \frac{\partial}{\partial r}+ \frac{\cos\phi\cos\theta}{r} \frac{\partial}{\partial \theta} -\frac{\sin\phi}{r\sin\theta}\frac{\partial}{\partial \phi} \)、いわゆる「チェインルール(鎖則)」である。これもまとめて、行列の形で表すことが可能である。
\[
\left(\begin{array}{c} \frac{\partial}{\partial x}\\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z}\end{array}\right)
=
J(r,\theta,\phi)
\left(\begin{array}{c} \frac{\partial}{\partial r}\\ \frac{\partial}{\partial \theta}\\ \frac{\partial}{\partial \phi}\end{array}\right)
\]
\(J=J(r,\theta,\phi)\)はヤコビアン(定義によってはヤコビアンの逆)である。
以上で、ベクトル解析における微分演算子(ナブラ演算子)\(\mathbf{\nabla}\)の極座標表現の計算に取り掛かる準備ができた。デカルト座標では
\[
\mathbf{\nabla} = \mathbf{e}_x\frac{\partial}{\partial x} + \mathbf{e}_y\frac{\partial}{\partial y} + \mathbf{e}_z\frac{\partial}{\partial z}=(\mathbf{e}_x, \mathbf{e}_y, \mathbf{e}_z)
\left(\begin{array}{c} \frac{\partial}{\partial x}\\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z}\end{array}\right)
\]と表すことができる。基底同士の線形関係式、および変数変換の関係式を、上式に代入すると
\[
\mathbf{\nabla} = (\mathbf{e}_r, \mathbf{e}_\theta, \mathbf{e}_\phi)
R(\theta,\phi)J(r,\theta,\phi)
\left(\begin{array}{c} \frac{\partial}{\partial r}\\ \frac{\partial}{\partial \theta}\\ \frac{\partial}{\partial \phi}\end{array}\right)
\]
であるが、真ん中の行列の積は、対角行列になって、
\[
RJ=\mathrm{diag}\left(1, \frac{1}{r}, \frac{1}{r\sin\theta}\right)
\]と計算される。
これでナブラ演算子が
\[
\mathbf{\nabla} = \mathbf{e}_r\frac{\partial}{\partial r}
+ \frac{1}{r}\mathbf{e}_\theta\frac{\partial}{\partial\theta}
+ \frac{1}{r\sin\theta}\mathbf{e}_\phi\frac{\partial}{\partial\phi}
\]となることが計算できた。
残りの計算は、ベクトル場を極座標で表した
\[
\mathbf{E}(\mathbf{r}) = E_r(\mathbf{r})\mathbf{e}_r + E_\theta(\mathbf{r})\mathbf{e}_\theta + E_\phi(\mathbf{r})\mathbf{e}_\phi
\]に、ナブラ演算子を作用させることである。いくつか面倒な点はあるが、それを乗り越えれば
発散\(\mathbf{\nabla}\cdot\mathbf{E}\)や、循環\(\mathbf{\nabla}\times\mathbf{E}\)など、極座標で表現された量を得ることができる。残りの詳しい計算は別紙に譲る(後日公開)。
[レポート課題1] 電気双極子のつくる電場を計算せよ。
[レポート課題2] ガウスの法則とクーロンの法則の関係について議論せよ。
[レポート課題] 非一様な電荷分布をもつ導体球と、電気双極子が等価であることを示し、
その周りに生成される静電場を計算せよ。
[レポート課題] ベクトル三重積の公式を導出し、その幾何学的な意味を議論せよ。
[レポート課題] グラスマンの力がアンペールの力と物理的には等価であることを示せ。
2016年度Aセメスター(木曜日2限)開講:理科I類(36,37,38組)
このページの目次
教科書:「電磁気学」砂川重信著
(岩波書店、物理テキストシリーズ4)[Su77]
日本の大学で広く採用されている標準的教科書。定理の証明などが丁寧に解説されている。
その一方で、数学的な詳細に惑わされ、物理的な側面が掴み難くいと感じる
人もいるかもしれない。
電磁気学の書き下し方は千差万別で、どの教科書を手に取ったらよいか
戸惑う初学者は多いはず。どの分野でもそうかもしれないが、とりわけ電磁気学の習得には、
一冊の教科書に頼るだけではなく、拾い読みしたり、比較したりするために、
複数の参考書を併用すべき。
参考書:
-
「ファインマン物理学:電磁気学」ファインマン、レイトン、サンズ著[宮島龍興訳]
(
岩波書店)[Fe69]
面白い比喩を用いたり、直感的な解説に基づいて、
「どうやったら物理的な思考ができるようになるか」種明かしのようなやり方で
物理を語ってくれる。また、時折披露してくれる独特の数学手法には、
おもわず唸ってしまうことも。一方で、標準的な学習項目を系統的に
網羅していないので、ところどころで別の教科書を用いて「予習」しておかなくては
読み続けることができないこともある。砂川の副読本としては最適。
砂川を読破した後に再度通して読めば、
電磁気のdeep insight(深淵?)に気付くことができるかも。
「電磁気学演習」砂川重信著(岩波書店、物理テキストシリーズ5)
[Su82]
「演習」とあるが、教科書本文とは異なる切り口で電磁気学を書き直している感じ。
「別の教科書」と見なしてもいいくらい。計算の詳細がさらに細かく記述されていて、
独習に役立つ。
「電磁気学I」太田浩一著 (丸善、物理学基礎コース)
[Ot00]
電磁気学の発展を正確に追った珍しいタイプの教科書。
多くの教科書で電磁気学をコンパクトに書き下そうとした結果、忘れ去られてしまった
重要な手法や概念を再発掘している。現在広く使われている様々な標準的な
教科書だけを読んでいると、なぜか納得できない、
「発想の飛躍」のように見える箇所があるが、そんな場所で
論理の鎖をつなぎ直してくれる「忘れられた式/概念」を見せてくれる。
「マクスウェル方程式から始める電磁気学」小宮山進、竹川敦共著(裳華房)
[Ko15]
駒場で電磁気学を30年以上教えてきた教官がたどり着いた、"The 駒場電磁気学"
とでもいうべき内容。クーロンの法則から始め、次第にマクスウェル方程式に
到達する標準的な教科書の流れを否定し、「初めにマクスウェル方程式ありき」
というスタイル。新しい教科書(2015年出版)だが、日本の「標準教科書」
になるかもしれない。
"Classical Electrodynamics (Third Edition)",
John David Jackson
(John Wiley and Sons, inc.) [Ja99]
アメリカ合衆国の大学院で広く採用されている、電磁気学の標準教科書。
電磁気学の教科書の「最高峰」といってもよいかも。ただし、この本から
電磁気を学び始めることはお勧めしない。初学者はあくまで参考書として
使用すべき。
多重極展開や変数分離による微分方程式の解法など、
量子力学で使う数学手法もこの教科書で学ぶ事ができるので、
量子力学をやってから戻ってきてもよいかもしれない。
「電磁気学―新しい視点にたって」バーガー/オルソン共著
(小林激郎/土佐幸子共訳)(培風館)[Ba92]
現代物理学における応用例が多く紹介されていて、それだけ見ても興味深い。
演習問題が豊富で、翻訳版には訳者による解答がついているのも嬉しい。
-
「物理のための数学」和達三樹著
(岩波書店)[Wa83]
電磁気学は電磁場を用いて記述され、その基本方程式であるマクスウェル方程式は、
ベクトル解析の技法によって表現されている。
したがって電磁気学の物理的側面を理解するには、
ベクトル解析に習熟しておく必要がある。しかし、物理と数学の知識を同時に習得するのは、
多くの初学生にとって苦労するところである。この本には、電磁気学で必要となる
ベクトル解析の計算法がコンパクトにまとめてあるので、辞書のようにして利用すると
効率的な学習が可能になるだろう。
以下の文章では、上記の教科書/参考書を引用するとき、本の題名の最後に付した記号、
例えば砂川先生の教科書は[Su77]、を用いることにする。
水素原子の場合について、重力とクーロン力の強度比を見積もってみる。
この考察の目的は、(i)クーロン力が重力に比べていかに「強いか」確認することと、
(ii)単位に気をつけながら物理量を計算する練習をすること。
簡単のため、ここで考える「水素原子」とは、
電子の軌道は円形(半径はボーア半径)とし、その中心に陽子が静止している系とする。
よく教科書に乗っている万有引力定数の値は、MKS単位系で
G=6.67×10-11 [Nm2/kg2]。
また、クーロン定数はk=(4πε0)-1
=c2/107
[Nm2/C2]である。c=3.00×108[m/s]は
光速の値である。単位[C](クーロン)は電荷量の単位で、
MKS単位系では[As](アンペア秒)に等しい。
電子に働くクーロン力FCと重力FGの強度比を計算すると、
FC/FG =
e2(4πε0)-1 /
Gmempとなる。
MKS単位系で、素電荷e=1.60×10-19[As=C], 電子の質量
9.1×10-31[kg]、陽子の質量1.67×10-27[kg]などを
代入し、丁寧に計算すれば答えは得られる。しかし、ここでは高エネルギー物理で
よく使われる電子ボルト(eV)の単位を利用して計算してみる。
eVはエネルギーを測る単位なので、MKS単位系における[J]=[Nm]と関連している。
1[eV]=e[J]である。
アインシュタインの関係式によれば、質量とエネルギーは等価で、E=mc2
となる。電子の質量エネルギーは0.5 [MeV]、陽子の質量エネルギーは
9.38×102 [MeV]〜1.0 [GeV] である。
[kg]で測った質量に光速の二乗をかけたmc2の単位は、当然MKS単位系
である。確認してみると、
[kg・(m/s)2] = [m・kg・m/s2]=[mN]=[J]となり、
エネルギーの単位をもつことがわかる。したがって、eVの単位は、
mec2/e=0.5×103[eV]=0.5[MeV],
mpc2/e=9.4×105[eV]=0.94[GeV]
という量に対して与えられる。
以上を踏まえて、FC/FGの表式をもう一度見ると、
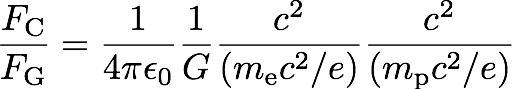
となる。(4πε
0)
-1=c
2/10
7
およびGの値を代入し、質量エネルギーの値を入れると
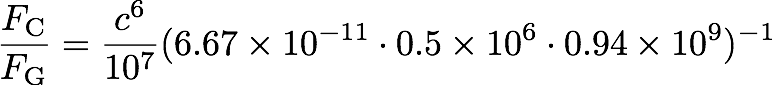
となる。これを数値計算するとF
C/F
G〜2.3×10
39
を得る。クーロン力の方が重力よりも圧倒的に強いことが確認できた。
高エネルギー物理を専攻する研究者は、電子の質量エネルギーが0.5MeV,
陽子の質量エネルギーが1GeV程度であることは記憶している。
また、物理学者ならc〜3.0×108[m/s]であることも覚えている。
したがって、クーロン定数が
c2/107であることを知っていれば、
万有引力定数を理科年表などで調べるだけでFC/FGを
簡単に見積もることができる。このような理由から、
高エネルギー物理学者は、上式のような変形を好む傾向がある。
実際に、Gだけを調べ、残りの物理量に関しては記憶している数値の精度で計算すると
FC/FG〜2.1(4)×1039となり、
正しいオーダーが得られるのはもちろんのこと、有効数字も1桁までなら正しく計算できる。
(古典)電磁気学において、古典力学で想定した「質点」に相当するのが、「点電荷」である。
大きさのない0次元の物体が電荷Qを保持しているというわけであるが、
その電荷はどこにどれだけあるのか?もし広がりのある3次元物体であれば、電荷密度ρに
よって電荷分布は示されるであろう。そしてその積分(体積積分)が全電荷Qになるはずである。
点電荷にも電荷密度の概念を拡張するならば、デルタ関数が必要になる。
デルタ関数を直感的に理解するために、有限な広がりを持つ電荷体から考察を始めてみる。
さらに、議論を簡易化するために1次元で考えてみる。ある場所x=x0を
中心に、おおよそ広さΔに渡って分布する電荷体は、ガウス関数(正規分布)G(x)によって
よく近似して表すことができる。このとき電荷分布はρ(x)=QG(x)と表すことができる。
∫ ρ(x) dx=Qだから、∫ G(x) dx=1、すなわちガウス関数は規格化されている。このため、
統計学ではガウス関数を確率分布として利用する。
この電荷体の密度がもっとも大きいのはx=x0だから、
∫ xG(x) dx = x0であるべきである(平均値)。
実際、ガウス関数はこの条件を満たす。
また、電荷体の広がりは大よそΔ程度であるから、
∫ x2G(x) dx - (∫ xG(x) dx)2〜Δ2
であるべきだが(分散値)、ガウス関数はこの条件も満たす。
上記のような条件を満たすガウス関数の具体的な形は、例えば
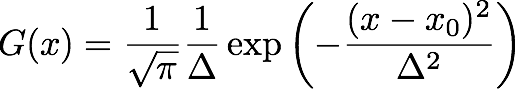
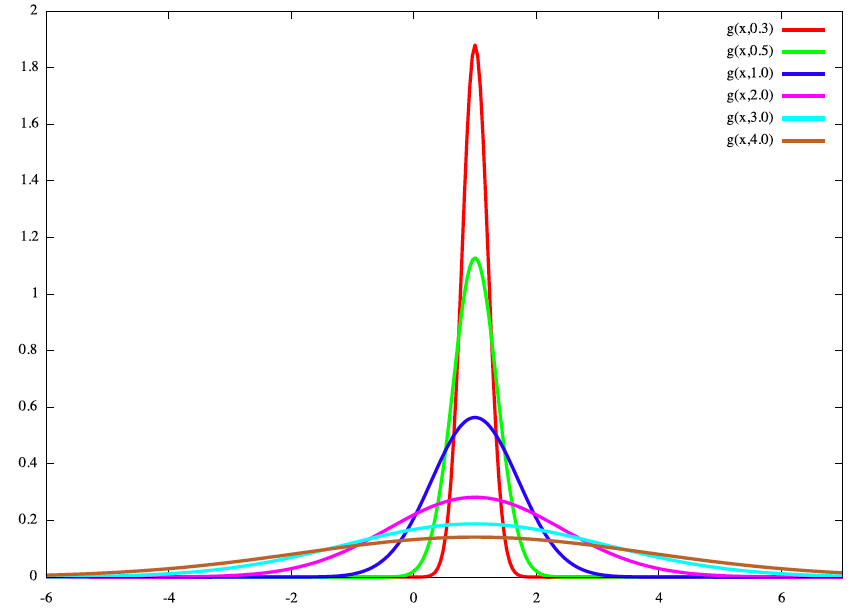
という形で与えられる。このガウス関数のグラフは下の図のようになる。
図では、x
0=1とし、Δ=4, 3, 2, 1, 0.5, 0.3の6パターンの場合を
重ねて表示している。
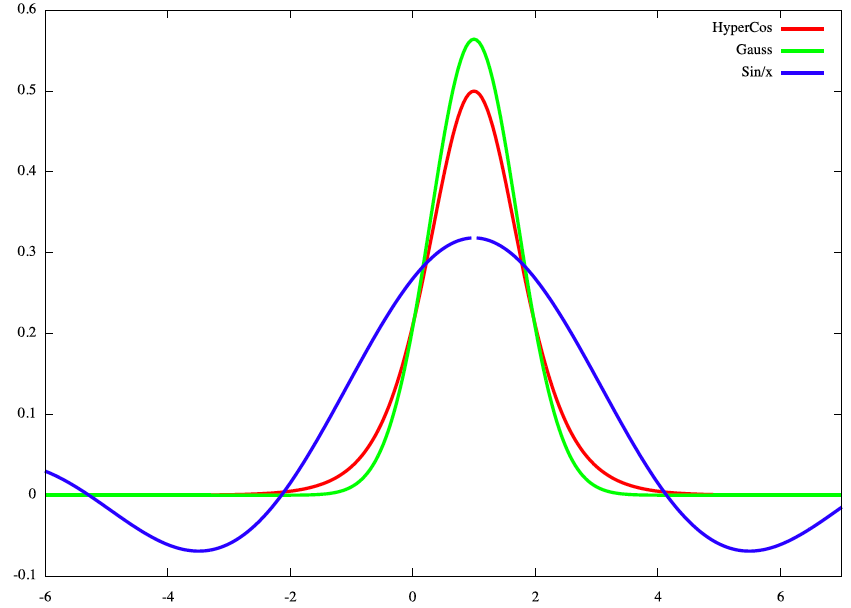
デルタ関数は、極限Δ→0におけるガウス関数として定義することができる。
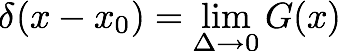
極限を取ってしまえば、どの関数系から始めても同じデルタ関数に到達することになる。
したがって、極限を取る前の関数には様々なものがある。どんな関数があるかは、太田先生の
教科書などを参照するとよい。[
Ot00, p.61の式(2.136)]
下図に、デルタ関数に収束する様々な関数系をプロットした。
どれも、同じ平均値(x0=1)、かつ同じ分散(Δ=1)をもつ。
具体的な表式は[Ot00]を参照のこと。
ガウス関数のように、デルタ関数が「電荷密度」を表すとすれば、少なくとも「規格化」
されていなくてはならないが、たしかにデルタ関数はその性質を満たす。
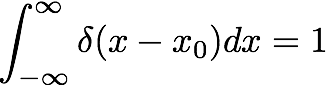
また、デルタ関数は次の性質も保持する。
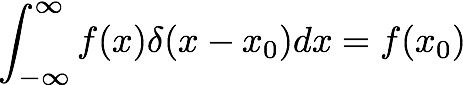
したがって、ガウス関数のように「デルタ関数の平均値」はx
0となる
(<x>=∫dx xδ(x-x
0),
つまりf(x)=xの場合に相当)。
また、デルタ関数の分散の二乗Δ
2は、デルタ関数の定義通り0となる(
Δ
2 = <x
2> - <x>
2,
右辺の初項はf(x)=x
2の場合に相当)。
3次元に拡張するときは、デルタ関数を次のように定義する。
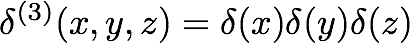
デルタ関数は、上記以外にも様々な性質や特徴があり、電磁気学にもたびたび登場する。
ローレンツ関数やラプラシアンを使った定義などについては、
講義でも触れることになるだろう。
任意のベクトル場Aの循環、curlA≡∇×Aは、
デカルト座標系において次のように表される。
ただし、ex, ey,
ezは、デカルト座標系における正規直交基底を表す。
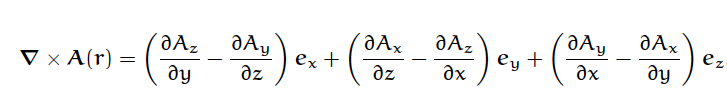 ...[1]
...[1]
デカルト座標における循環の表現では、その成分が反対称性を持っている。
加えて、成分同士は、添字に関してのcyclicな置換によって関連づけることができる。
総じて、ベクトル場の循環は、デカルト座標系において「美しい」形をもっているといえる。
一方、「回転する
Death Starディスプレイ」の問題(これは電磁誘導の練習問題のひとつ)
のように、円筒座標を導入した方が計算しやすい場合もあるので、
円筒座標における表現でベクトル場の循環を書き下すことを考えてみよう。
結論からいうと、円筒座標におけるベクトル場の循環は次のようになる。
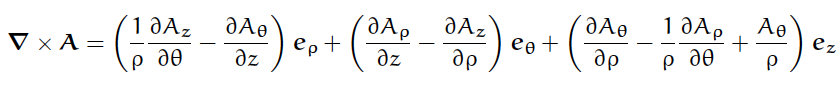 ... [2]
... [2]
円筒座標における正規直交基底は
eρ=
t(cosθ, sinθ, 0),
eθ=
t(-sinθ, cosθ, 0),
ez=
t(0,0,1)で与えられる。
各成分をみると、円筒座標系では循環の(成分の)反対称性が失われてしまうことがわかる。
しかも、z成分の中に、微分で表されない項A
θ/ρが現れるため、添字の置換に
対する対称性の破れ具合がひどくなっているのが特徴的である。
式[1]から式[2]への変形は、ベクトルの座標変換、基底変換、そして微分の変数変換を
まとめて(正直に)行えば得られるが、計算は煩雑になる。ここでは、
微分演算子∇を円筒座標で書き直してから、円筒座標で表したベクトル場Aに
直接作用させるやり方で導出してみよう。
微分演算子∇の表現
微分演算子∇は、ベクトルのように3つの成分をもち、それらが偏微分で表されると考えると、
∇は次のように表す事ができる。
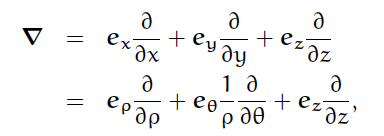
上の行の式がデカルト座標系における表現、下の行が円筒座標系における表現である。
上から下への変換は、偏微分の変数変換および基底変換によって得ることができる。
以下では、円筒座標系における表現、すなわち下の行の式を採用する。
次に、ベクトル場の円筒座標系における表現は
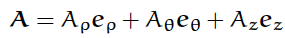
となるから、ベクトル場の循環の計算は
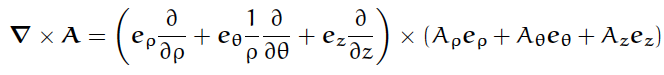 ...[3]
...[3]
となる。これを直接計算すれば、上式[2]が得られるはずである。
この演算で気をつけるべきなのは、基底の微分である。円筒座標や極座標における基底は
座標に依存する成分を持つので、微分がnon-vanishingの場合があり注意を要する。
円筒座標の場合は、次の2つの微分が寄与してくる。
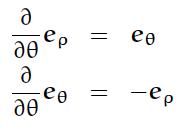
円筒座標系の基底に関するその他の微分は皆ゼロベクトルとなる。
上式[3]にはeid×Ak(r)
ejといったタイプの計算が何回も現れる。
(dはなんらかの変数に関する偏微分演算を意味する記号とする。)
ベクトルを、デカルト座標系の成分表示にしてから、丁寧に外積の計算をすると、
このタイプの計算の結果、2つの項が現れることがわかる。すなわち、
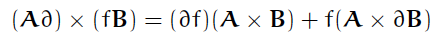
A,Bはベクトル場、fはスカラー場を表し、それぞれ位置
rに依存する。
円筒座標系の基底において、その微分が効いてくるのは上述したように2つの場合だけである。
すなわち、上の公式において第二項が残るのは2つの場合に限られ、
残りは第一項だけが寄与する。第一項は基底同士の外積であるから計算は簡単である。
公式の第二項が寄与する計算は
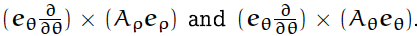
である。たとえば、最初の計算に公式を適用すると
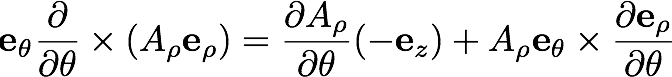
となるが、左辺第二項の基底の微分は
eθに等しいから、
自分同士のベクトルの外積は0となる性質を思い出すと、第二項はvanishする。
こんな具合に計算を進めていくと、円筒座標系におけるベクトル場の循環の式[2]が
得られる。
2016年の期末試験の問題I(3)に対する訂正。
誤:「任意のベクトル場A(r)により、eφ=∇×A(r)と表せることを示せ。」
正:「eφ=∇×A(r)を満たす
ベクトル場A(r)が必ず存在することを示せ。」
関連資料のダウンロード [pdf(98kB)]
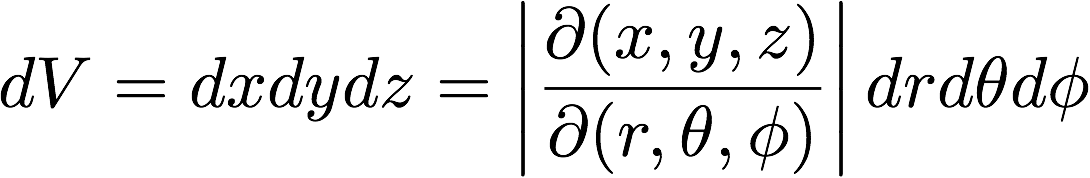
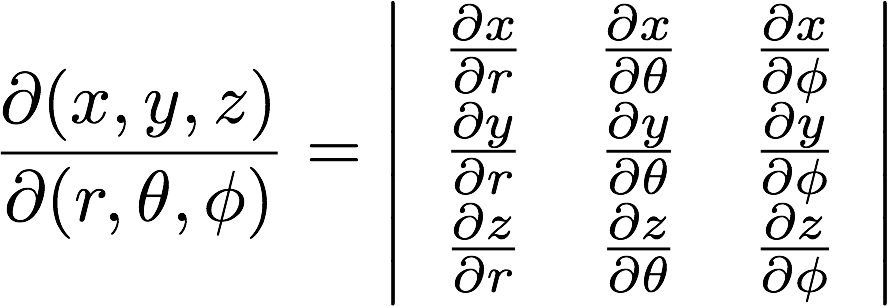
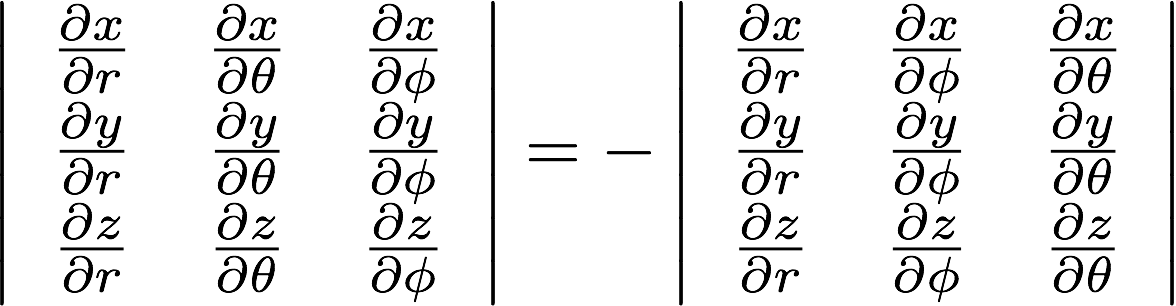
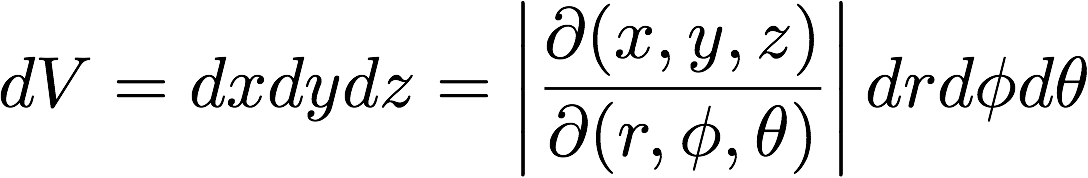
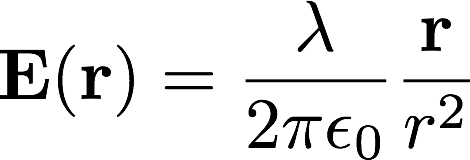
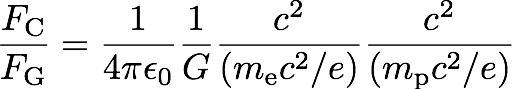
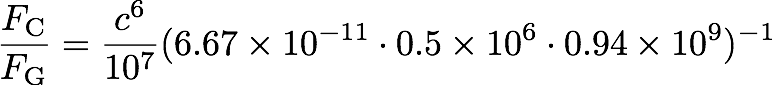
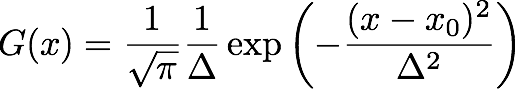

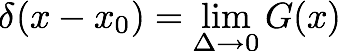

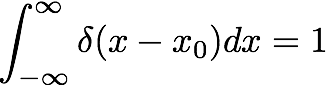
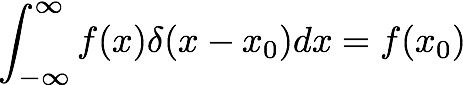
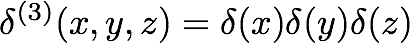
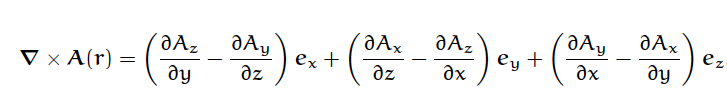 ...[1]
...[1]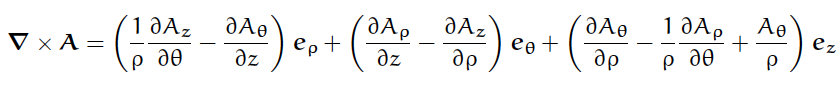 ... [2]
... [2]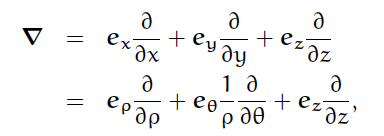
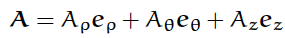
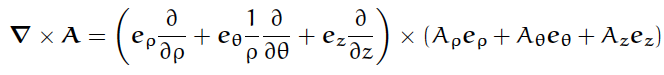 ...[3]
...[3]