Usage: Fuzzy Measure-Choquet Integral Calculation System ( λ fuzzy measure and sensitivity analysis)

The purpose of this site (http://www.isc.senshu-u.ac.jp/%7ethc0456/Efuzzyweb/fm11.html) is to understand Choquet Integral using λ fuzzy measure. This software caclate the Choquet integral using λ fuzzy measure by CGI. If you calculate Choquet Integral a lots of times, I recommend to use Fuzzy Integrals(Multipurpose).

"λ Fuzzy Measure Identification Methods using λ and Weights (PDF file)" is the theoretical summary of Choquet integral with λ fuzzy measure.

Functions

• Identifications of λ fuzzy measure
• Choquet Integral
• OUTPUT: TEXT FILES, GNUPLOT FILES, EPS FILES
• Sensitivity Analysis

Example

It is Global evaluation model to buy a new car like AHP model. Evaluation items are "Price", "Performance", "Design" and "Fuel-efficiency". The evaluation objects are 4 cars, "C1", "C2" and "C3". Individual evaluation scores are given as in Table 1. For example, these scores are calculated by pair-wise comparison of AHP.

Table 1. Individual evaluation scores

Car	Price	Performance	Design	Fuel-efficiency
C1	0.2	0.3	0.3	0.4
C2	0.1	0.2	0.2	0.3
C3	0.1	0.5	0.5	0.3

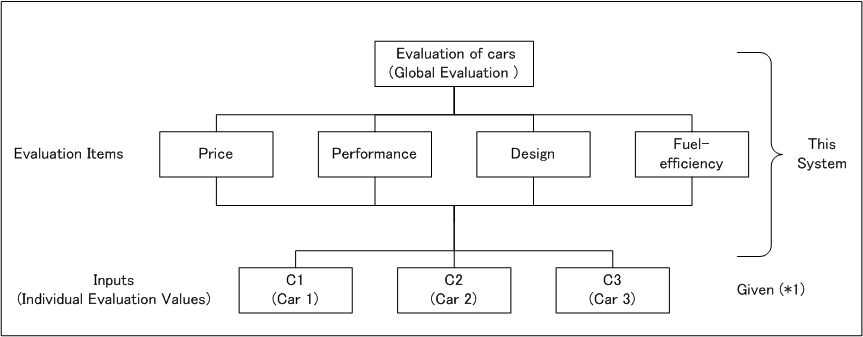
Hierarchy Diagram (Example)

*1 :The input values are given values in this system. You can identify the input values ordinal pairwised comparison method using the calculation site (http://www.senshu-u.ac.jp/~thc0456/Eahp/)

Fuzzy AHP (Fuzzy Integral Based AHP)

This system can calculate the Fuzzy Integral Based AHP(Fuzzy AHP). Fuzzy Integral Based AHP model and HFI (Hierarchy Fuzzy Integral) model are the new calculation using Choquet Integrals. The models use Choquet integrals instead of ordinal weighted sum and enable to do global evaluation with interaction degree among evaluation items, such as "Positive evaluation", "Negative evaluation", "Balanced evaluation" and so on. The parameters of the model are evaluation items weights and interaction index.

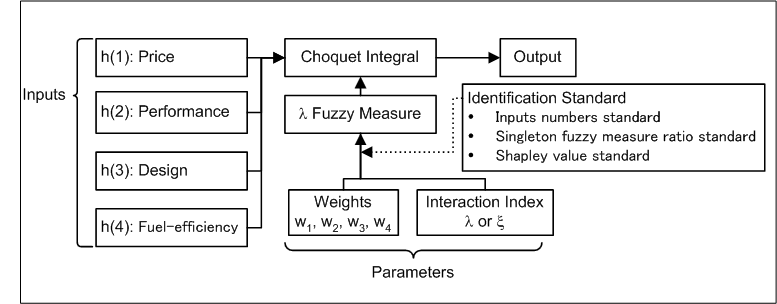
Choquet integral with λ fuzzy measure (Example)

INPUT: n( number of Evaluation Items) and m (number of Inputs)

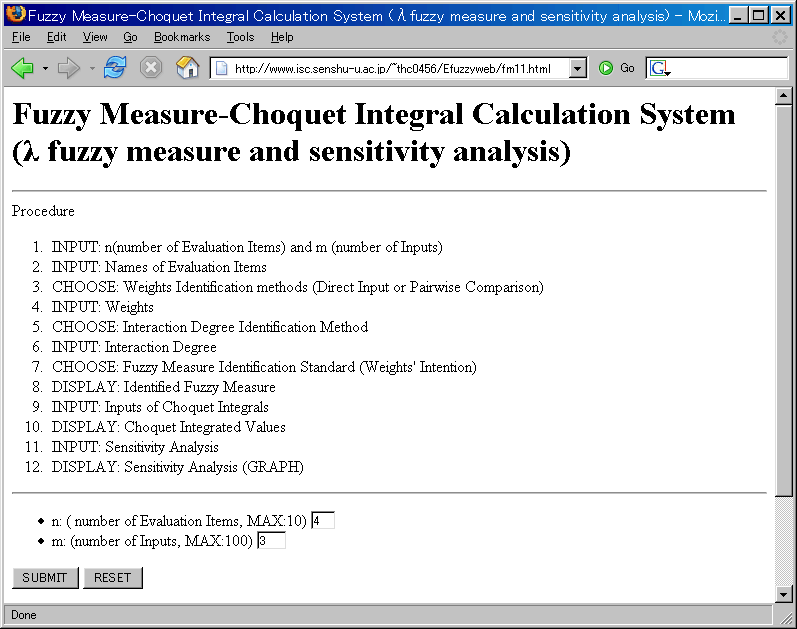
Number of Evaluation Items (n)(MAX:10)

Example: 4, because evaluation items are "Price(PR)", "Performance(PE)", "Design(D)" and "Fuel-efficiency".

Number of Inputs (m) (Max: 1000)

Example: 4, because number of evaluation objects are 3, "C1", "C2" and "C3".

Restriction

n * m ≤ 5000

INPUTS: Names of Evaluation Items

If you do not input theses fields, the number is used

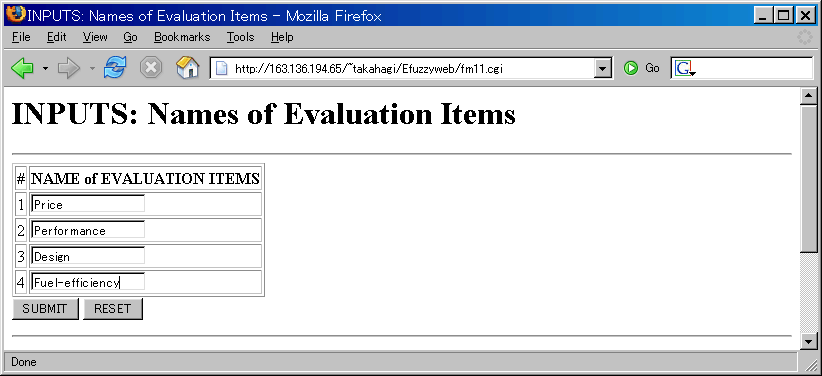
Example: "Price", "Performance", "Design" and "Fuel-efficiency"

Choose: Weights Identification methods

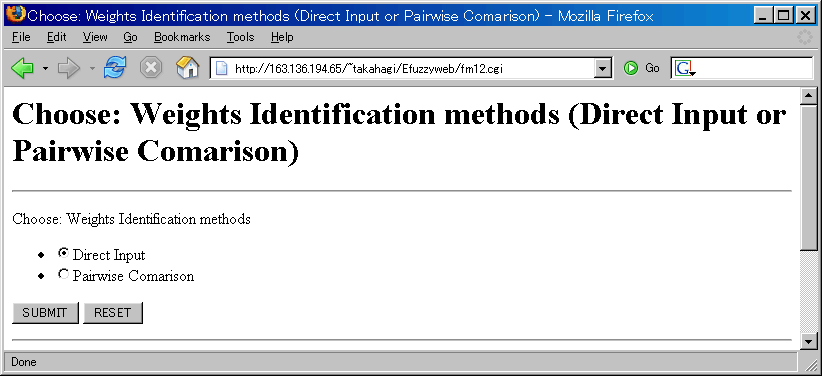
Direct Input

you can set the weights directly

Pairwise Comparison

You can set the weights using Pairwise Comparison (like AHP).

INPUTS: Weights (Direct Input)

If you select the "Direct Input", following page is displayed.

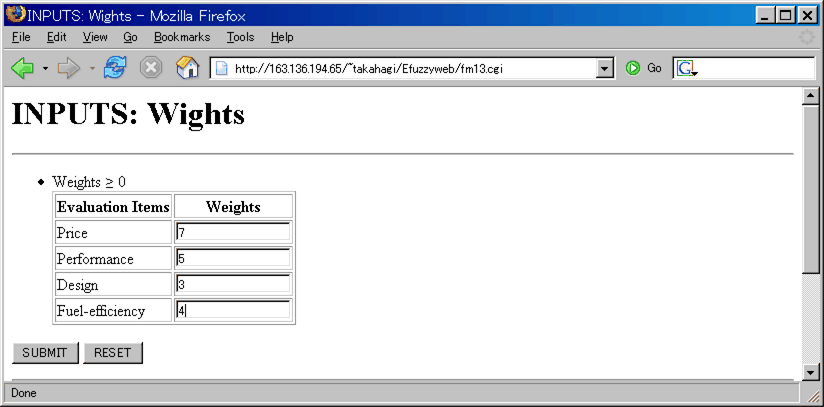
Input values must be non-negative values

Example: "Price" weight is 7, "Performance" is 5, "Design" is 3 and "Fuel-efficiency" is 4.

INPUTS: Weights (Pairwise Comparison)

If you select the "Pairwise Comparison", following page is displayed.

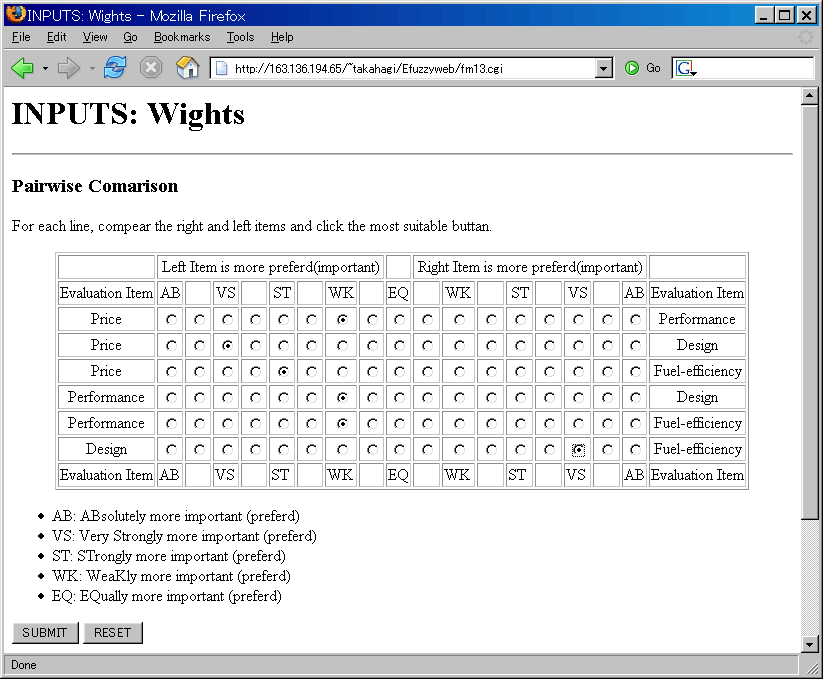
All combinations of evaluation items must be compared

Example

• 1st line of radio buttons: Pairwise Comparison between "Price" and "Performance". If "Price" is weakly more importance than "Performance", then check the left side "WK" field.
• 2nd line: Pairwise Comparison between "Price" and "Design". If "Price" is very strongly more important than "Design" then check the left side "VS" field.
• Bottom line: Pairwise Comparison between "Design" and "Fuel-efficiency". If "Fuel-efficiency" is strongly more important than "Design" then check the right side "ST" field.

Click the "SUBMIT" button, then the Pairwise Comparison Matrix and the identified weights are shown.

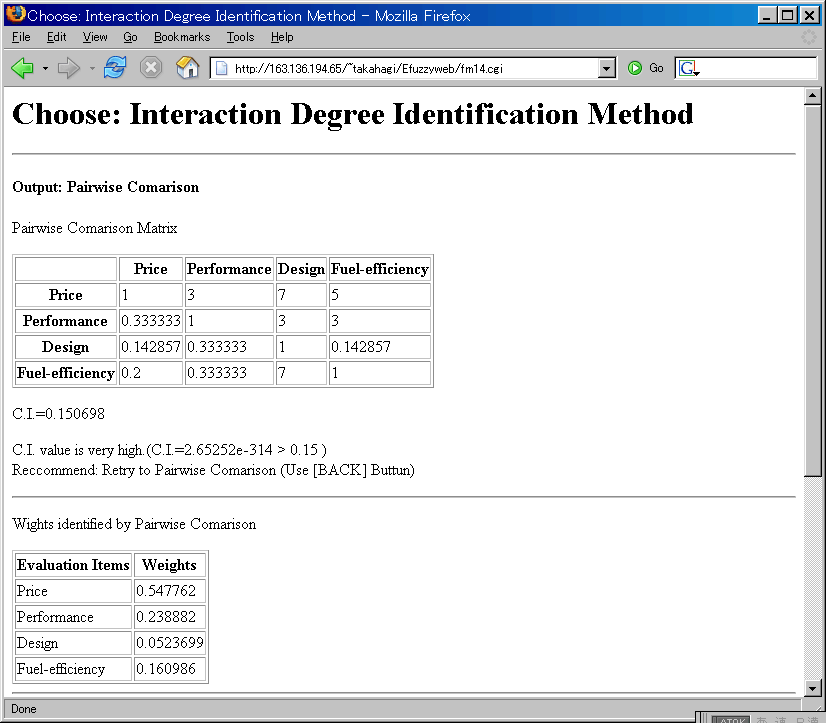
The result of Pairwise Comparison

If the message "C.I. value is high" is shown (C.I. > 0.15) , you should retry the Pairwise Comparisons, because your Pairwise Comparisons include the contradiction(s).

Choose: Interaction Degree Identification Method

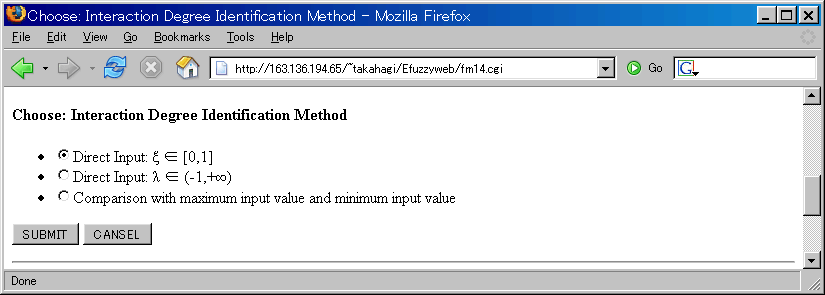
In this web site, two interaction degrees λ and ξ are used.

Direct Input: ξ ∈ [0,1]

ξ	0	0 < ξ < 0.5	0.5	0.5 < ξ < 1	1
Identify Standard	Inputs numbers standard	All standards	All standards	All standards	Inputs numbers standard
Fuzzy Measure	g(A)=0 (A ≠ ∅)	Super additive	Additive	Sub additive	g(A)=1 (A ≠ X)
Aggregation Method	Minimum	Intermediate Aggregation between minimum and weighted sum	Weighted Sum	Intermediate Aggregation between maximum and weghted sum	Maximum
Kansei Words		Complementary		Substitute
		Balance		Personality
		Negative		Positive
		Cautious		Daring
		Conservative		Progressive
		Certainty		Possibility

Direct Input: λ ∈ (-1,+∞)

λ	-1 < λ < 0	0	0 < λ
Fuzzy Measure	Sub additive	Additive	Super additive
Aggregation Method	Intermediate Aggregation between maximum and weighted sum	Weighted Sum	Intermediate Aggregation between minimum and weighted sum
Kansei Words	Substitute		Complementary
	Personality		Balance
	Positive		Negative
	Daring		Cautious
	Progressive		Conservative
	Possibility		Certainty

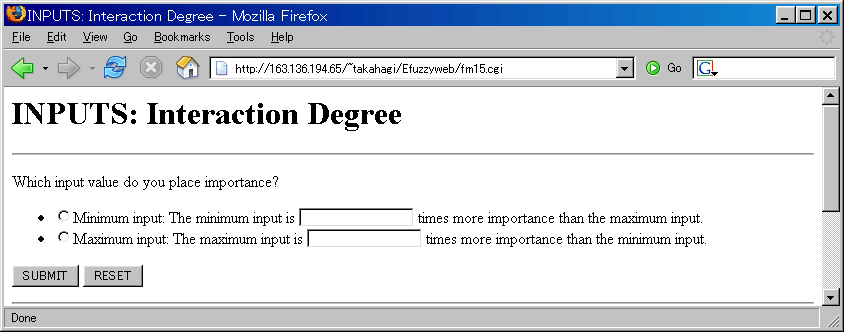
Comparison with maximum input value and minimum input value

The interaction degrees are identified by the importance ratio between maximum input value and minimum input value. First, you select which input value is importance. If you select minimum input values, it means you select super additive fuzzy measure. If you select maximum input values, it means you select sub additive fuzzy measure.

Second, you select how much times you put importance. The value is bigger, the output is closer to maximum or minimum input.

Choose: Fuzzy Measure Identification Standard (Weights' Intention)

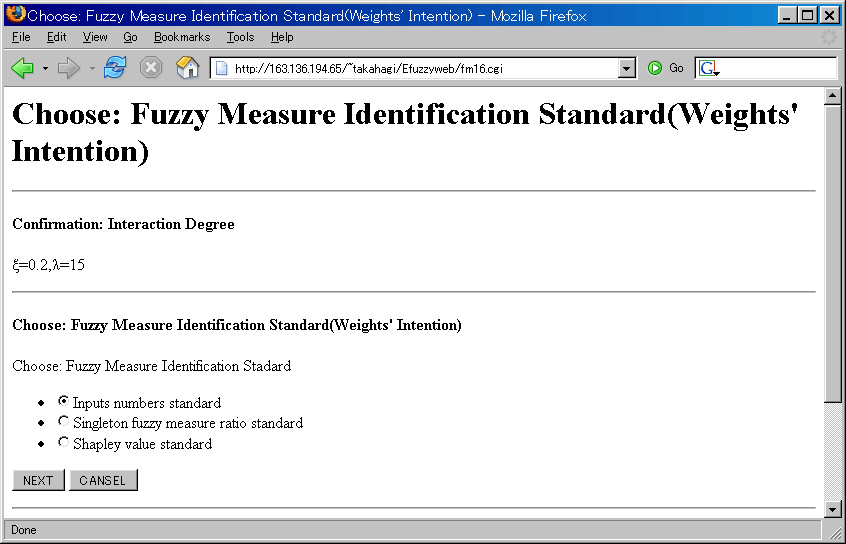
Inputs numbers standard (Recommend)

Weights intention is the number of inputs. For example, if "Price" weight is 7, Performance is 5, Design is 3 and "Fuel-efficiency" is 4, then there are 19 the same weight input items and 7 out of 19 are "Price" inputs, 5 out of 19 are "Performance", 3 are "Design" and 4 are "Fuel-efficiency".

Singleton fuzzy measure ratio standard

g({1}):g({2}):...:g({n}) = w₁:w₂:...:w_n

Shapley value standard

Sh_i:i-th Shapley value of g

Sh_i=w_i, i=1,2,...,n where ∑ Sh_i = 1

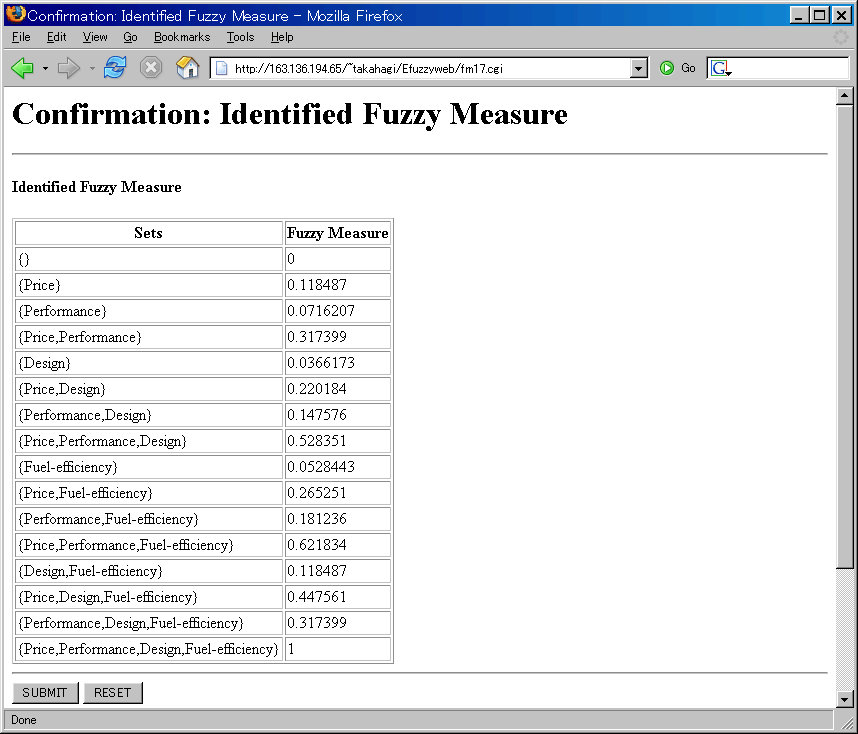
Confirmation: Identified Fuzzy Measure

INPUTS: Inputs of Choquet Integrals

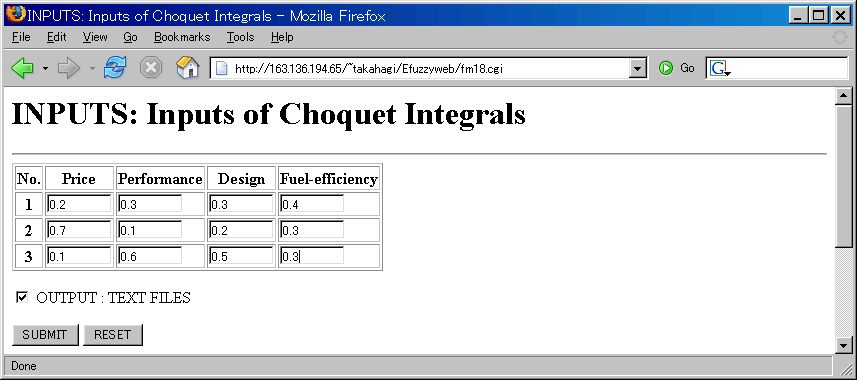
• You can identify the input values by pairwaise comparison system . However, it is not nessesary to identify the input values by Pairwise comparison.
• If you check "OUTPUT: TEXT FILES", you can get a text file of Choquet integrated values.

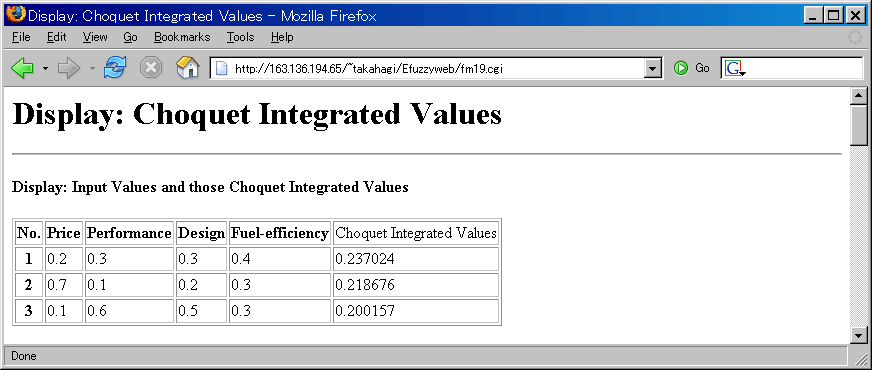
Display: Choquet Integrated Values

SETTING: Sensitivity Analysis

This Sensitivity Analysis system enable to get graph with varying interaction index ξ or λ.

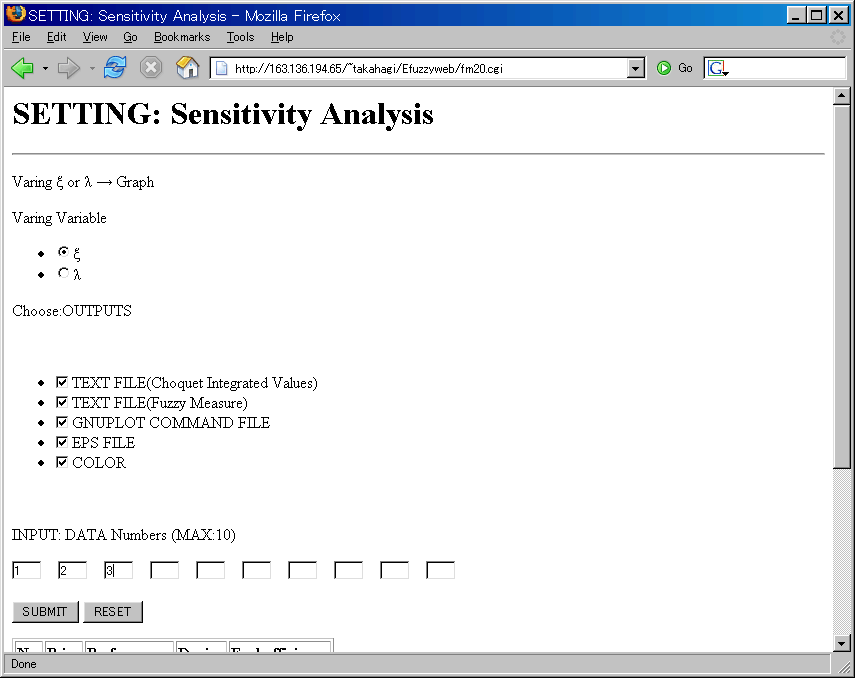
Varying Variable

Please set ξ or λ

INPUT: DATA Numbers (MAX: 10)

Only set number's data are displayed.

Example: Evaluation objects are 3, so all the objects are set,1, 2 and 3.

Display: Sensitivity Analysis

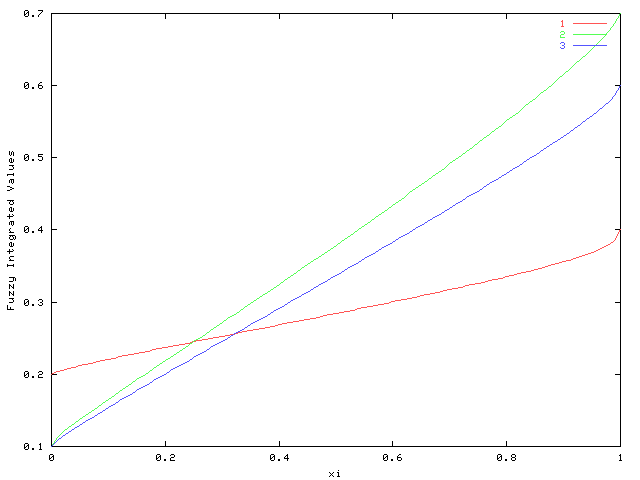
Varying ξ (Colour)

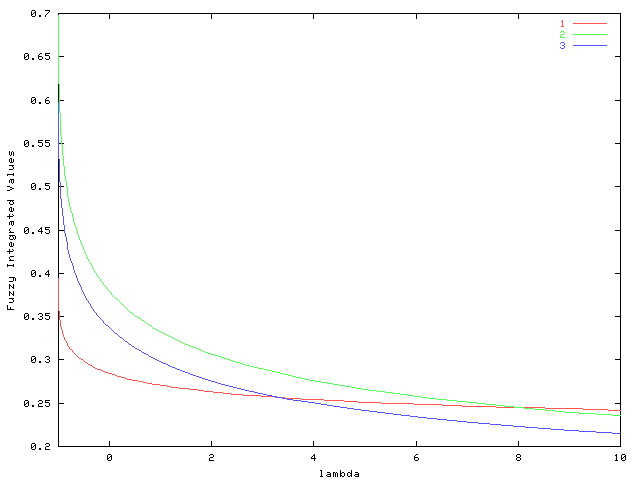
Varying λ (Colour)

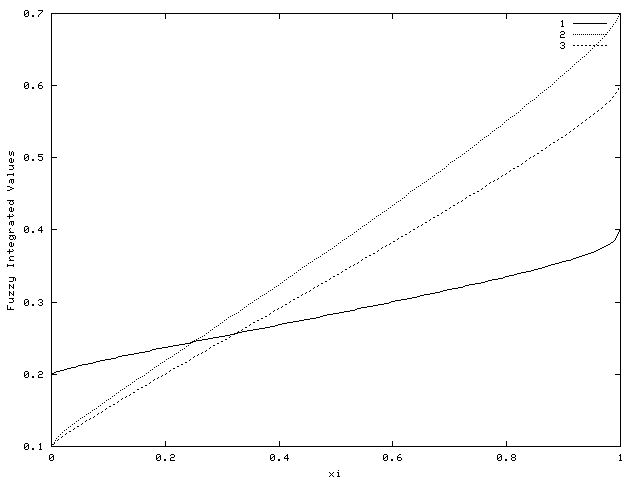
Varying ξ (Monochrome)

From the "Varying ξ (Colour)" graph, C1 (Red line) is most preferred car when ξ < 0.25, that is, the evaluator place importance strongly the balance among evaluation items. In the other cases, ξ > 0.25, that is, the evaluator do not place importance strongly the balance among evaluation items, C2 (Green line) is the most preferred car.

Reference

• [1] Takahagi, Eiichiro: An intermediate Evaluation Method among Maximum, Average and Minimum using Fuzzy Measure and Choquet Integral and its Applications, "Methodologies for the conception, design, and application of intelligent systems; proceedings of the 4th International Conference on Soft Computing 1", World Scientific, 299-302, iizuka, 1996.
• [2] Takahagi, Eiichiro: On Identification methods of λ-fuzzy measures using weights and λ, Japanese Journal of Fuzzy Sets and Systems, vol.12, no.5, 665-676, 2000 (Japanese).
• [3] Eiichiro Takahagi: λ Fuzzy Measure Identification Methods using λ and Weights (PDF file) (English summary of the paper [2] to shows the fuzzy measure identification methods using λ and those algorithms)

• If you want to change the some values, please use [Back] button.
• You can use this CGI system from http://www.isc.senshu-u.ac.jp/%7ethc0456/Efuzzyweb/fm11.html
• Fuzzy Integral Calculation Site (Fuzzy Integrals and Fuzzy Measure)
• Contact: takahagi@isc.senshu-u.ac.jp

© 2005 Eiichiro Takahagi