力学A(東京大学前期課程)の講義情報
2018年度Sセメスター(水曜4限)開講:理科II,III類(16,17,18組)723教室
このページの目次
- 教科書/参考書
-
[はじめに]
力学を学ぶ理由(数理的手法で自然科学を記述すること)
-
[第一回] 数理的手法による物理学の記述 [Apr 11]
-
[第二回] 微分・積分を導入する [Apr 18]
-
[第三回] Taylor/Maclaurin展開の応用[Apr 25]
-
[第四回] 極座標の導入[May 2]
-
[第五回] 極座標の応用と線形代数の概念[May 9]
-
[第六回] 調和振動子とケプラー問題[May 16]
-
[第七回] ケプラー問題の続き[May 23]
-
[第八回] シュレディンガーの「生命と物理」[June 6]
-
[第九回] 減衰振動 [June 13]
-
[第十回] エネルギー保存則(3次元) [June 20]
教科書: 戸田盛和
(岩波書店、物理テキストシリーズ4)[Td82]
戸田先生は、「戸田格子(Toda Lattice)」の提唱者として広く知られている。戸田格子とは、
非線形な復元力をもつバネを連結した多体系であるが、
戸田先生はこの非線形力学模型を1967年に提唱したのみならず、
その運動方程式は可積分であることを証明した(解は楕円関数を使って記述される)。
古典力学の非線形可積分問題(およびその解)の発見は、
コワレフスカヤのコマ(剛体の回転運動を取り扱った力学模型)以来となる、ほぼ八十年ぶりの偉業である。
古典力学は「すでに完成しており、『死んだ』学問(つまり新しい発見はもうない)」と思われがちであるが、
NatureやPhysical Review Lettersなどにも、いまだに時折新しい論文が掲載されることがある。
これはにはカオス力学の近年の発展も助けとなっている。
古典力学は、いまだに「進歩し続ける」学問とみなしてよいだろう。
面白いことに、戸田先生の教科書には調和振動子関連の記述があまりない(典型的な調和振動子の説明はある)。
強制振動とか、減衰振動は省略されている。ご自身が発見した「戸田格子」の説明もなければ、非調和振動子に
関するコメントもない。その代わり、「おもちゃ」の力学を取り扱ったコラムが散りばめられている。
猫の宙返りや、回転椅子の説明はとても面白い!
参考書:原島鮮「力学Iー質点、剛体の力学ー」(裳華房) [Hr73]
1972年に出版された「古い」教科書である。が、多くの大学で採用されている「標準教科書」でもある。
細かい計算の解説がある一方で、細かすぎて議論の大筋を見失いがちになる傾向もある。必要な概念/内容
を拾い読みするとよいかもしれない。
参考書:ファインマン、ゴットリーブ、レイトン(戸田盛和、川島協訳)
「ファインマン流物理がわかるコツ」(岩波書店2015年)[FeGd15]
カリフォルニア工科大学(カルテク)の物理の講義から落ちこぼれそうな学生に向けて開かれた「補講」の内容を
まとめた教科書。大学の物理にいまひとつ馴染めずに困っている人は、読んでみるといいかもしれない。
ちなみに戸田先生はファインマンと私的な交流があり、駒場の博物館で戸田先生の遺品が展示されたとき、
ファインマンが訪日中に戸田先生宅を訪れたときに書いた「落書きの墨書(ファインマンダイアグラムも描かれていた)」も出品されていた。
友人の教科書を翻訳するのは楽しい作業だったはずだ。(訳者あとがきには、
カルテク出身の川島先生が翻訳作業を主導し、戸田先生は細部をチェックしたとある。)
参考書:シュレディンガー(岡小天、鎮目恭夫訳)「生命とは何か」
(岩波文庫2008)
[Sh08]
量子力学を完成させたシュレディンガーは、物理学の観点から生命のいくつかの特質、
例えば、なぜ原子よりも大きいのか、
熱力学の第二法則に反して(比較的)長い寿命を持ちうるのか、などについて理論的な考察を行った。
それはもともとは一般向けの講演のための考察だったのだが、この講演内容をまとめた本書は
その後の生物学に多大な影響を与えた。とりわけ、DNAの二重螺旋構造を解明したワトソンは
シュレディンガーの本を読んで分子生物学を志したという話である。
物理学に基づくミクロ/マクロの観点から生命体の性質を物理的に考察する方法論は、生物学の枠組みだけで
生物学を取り扱うアプローチではたどりつけないような事柄を発見するのに大いに役立っている。
この本を読むためには、古典力学の「因果性」、統計力学の「平均値の意味」、そして量子力学の「確率性」
の3つを理解している必要がある。分子生物学を志す学生がこの本を読むのは必須だと思われるが、
力学Aでは最初の鍵「因果律」について学ぶことができる。
参考書:ワトソン(江上不二夫、中村桂子訳)「二重らせん」
(ブルーバックス2012)
[Wa12]
DNAの二重螺旋構造を解明しノーベル賞を受賞した著書から見た、その発見経緯を綴った記録。
主にポーリングとの競争について書かれており、勝負はX線回折像の数理モデルの分析にあったことが
語られている。その緊迫する日々の研究の様子には引き込まれるものがある。ただ、肝心のX線解析画像を
高品質で撮影することに成功したフランクリンに対する言及が少ないことが指摘されている。
実は、この画像の入手の経緯を巡って論議があり、ワトソンは一部の科学者から「剽窃」の
疑いをかけられていることは知っておくべきだろう。ちなみに、フランクリンはノーベル賞をもらうことは
なかった。受賞前に早死にしたから(実験のためにX線を浴びすぎたという説もある)とか、
男女差別があったからとか、いろいろ言われている。
戸田の教科書[Td82]の「はじめに」に書いてあるのが、力学を学ぶ理由である。
主な内容を抜き出してみると、
(ii) 自然現象を数理的に扱うことを学ぶ。
(iii) 電磁気学(や量子力学)など、他の物理学の基礎として学ぶ。
とある。本講義では、この方針に沿って力学を展開したいと思う。
目標: 自然科学の記述として数理的手法を用いる方法論を習得すること。
題材: 質点の運動(=いわゆる「動力学」(Dynamics)とよばれるもの)、および
その応用(二体問題と剛体)。
研究者になるための基礎トレーニングが終了し(つまり駒場での教養過程が修了し)、
研究者への階段を登り始めると、
より複雑な多体問題や、流体、弾性体などの力学を扱うようになるだろう。
たとえば、血管中を流れる血液のシミュレーションや、血栓が血管中をどのように流れて梗塞を
引き起こすかを分析するシミュレーションやその数理モデルの開発、あるいは人工軟骨の弾性性能の分析や
ロボット義足の力学的性能の見積もりなど、面白そうな研究のネタはたくさん転がっていそうである。
研究者となってこれらの問題にたち向うとき、生物学や医学のアプローチのみにとらわれず、
力学の基礎に立ち戻って立ち向かうのが大切になるだろう。
実際、DNAの二重螺旋構造を発見したWatsonとCrickは
物理や数理の手法に長けていたし、そのライバルだったPaulingも化学と量子力学を結びつけ、量子化学を
編み出したところに成功のポイントがあった。
さらには、量子力学を完成させた一人、Schrodingerは
「生命とはなにか」という名著を残しているが、これは物理学の観点から生物系を議論した最初の本である。
生命の代謝に相当する「負のエントロピー(これは現代の観点から否定されているが)」の議論や、
生命体の基本単位である細胞が、小さいけれど小さすぎない理由は、不確定性原理に従う生命システムは
長生きできないからである、という論点は興味深い(生命システムは、
因果律がなりたつ古典力学が成立する程度に「大きい」物体でなくてはならないのである)。
Watsonはこの本を読んで、分子生物学を志したという話である。
高校物理では、ベクトル、行列はもちろん、微分積分、そして微分方程式など、物理学で必要な
数理手法がすべて抜け落ちている。大学で学ぶ力学では、まず高校物理で「歪められた」
本来あるべき物理学の姿を紹介することから講義を始めることが多い。たとえば、
運動方程式は、高校物理ではF=maと習い、もっぱら初等的な四則演算だけでこの方程式を処理するが、
大学で扱う運動方程式は次のような形、すなわちベクトル量に対する微分方程式、になる。たとえば、
減衰振動を表す運動方程式は
\[
m\frac{d^2}{dt^2}\mathbf{r}(t) = - m\omega^2\mathbf{r}(t) -2m\gamma\frac{d}{dt}\mathbf{r}(t).
\]
という形で与えられる。この方程式は「微分方程式」になっているので、積分することで解,すなわち
\(\mathbf{r}(t)\)の具体的な形を求めることになる。運動方程式は、2階の微分量を含むので、
2階の微分方程式であり、積分を二回行うことで解を得ることになる。
ちなみに、
大学の物理では、ベクトル量は矢印\(\vec{A}\)を用いて表記する場合もあるが、太字\(\mathbf{A}\)で
表すこともある(東大では後者を採用する研究者が多いと思われる)。
ベクトルを使った方程式の表現も、高校の物理ではあまり推奨されない。「記号」としては出てくるが、
実際の問題では最初から成分に分解した結果から解き始めることが多い。たとえば、下のような斜面を滑り落ちる
積み木の問題を例に考えてみたい。
 (Wikipediaより引用)
(Wikipediaより引用)
高校の物理では、最初から斜面の方向と、それに鉛直な方向に力の成分を分けて方程式を立てる。
前者は運動方程式として、後者は釣り合いの方程式として扱う。問題を解く、という観点からすれば、
この方法は有効であり、なんの問題もない。しかし、どうして2つの成分に分けて
考えなくてはならないのだろうか?3つとか、4つにならないのはどうしてなのだろうか?
力はベクトル量である。今考えている問題は「2次元平面」であることを考慮すると、
運動方程式に使うべき力は2次元のベクトル量として表すことになる。重力を\(\mathbf{F}_g\),
垂直抗力を\(\mathbf{N}\)と表すとすれば、高校で習う運動方程式\(F=ma\)を、ベクトルを使って表すと
\[
m\mathbf{a} = \mathbf{F}_g+\mathbf{N}
\]
となる。(斜面が静止しているようにみえる)慣性系において、水平方向と鉛直方向にxy座標(デカルト座標)
をとることにする。上の運動方程式を成分で表すと、
\[
m\left(\begin{array}{c}a_x\\ a_y\end{array}\right)
=
\left(\begin{array}{c}0\\ -mg\end{array}\right)
+
\left(\begin{array}{c}N_x\\ N_y\end{array}\right)
\]
となる。
2次元平面のベクトルの成分は2つである。運動方程式は、このベクトルの間の関係式である。
したがって、扱う方程式の数は2つになるのである。数学的には、線形代数における「n次元ベクトル空間に
おける1次独立な基底の数」に関わる定理によって説明されるべきことがらである。物理では、この数を
「運動の自由度」と呼ぶことがある。(たとえば、「剛体の定義から、剛体の自由度が6であることを証明せよ」
というのはよくある問題の一つである。)
ところで、暗黙の了解として、積み木は斜面に沿って運動するという仮定がある。
つまり、積み木は、斜面から飛び跳ねたり、斜面にめり込んだりはしないという「拘束条件」である。
この拘束条件により、積み木の運動は実質的には(2次元平面内の)1次元運動となる。
(しかし、上の方程式の表現では、まだ2次元的な運動のように見える。)
実質は1次元運動である、ということを利用するには、最初に定義したデカルト座標を回転させ、
斜面に沿った方向にx軸が重なるようにすればよい。座標系の選択は任意であり、問題を解く際には
自由に選ぶことができる。座標を回転させるには回転変換を採用するが、それはベクトルを回転させる
という操作とみなすこともできる。この問題で採用すべき回転変換は次のような2x2の行列によって
表現される。
\[
R(\theta)=\left(\begin{array}{cc}\cos\theta & \sin\theta\\ -\sin\theta & \cos\theta\end{array}\right).
\]
最初に作った運動方程式の両辺にこの回転行列を作用させると、高校で習った方法で出てくる方程式が
得られる。つまり、高校では「首をかしげて」2次元の問題を解いていた、ということである。
行列には、積と和の演算が定義されている(これを数学では「代数」という)。
行列の最大の特徴は、積が非可換であることである。例えば、A,Bをn次元の正方行列とすると
\[
AB \ne BA
\]
この性質は、物理では「量子力学」で重要な役割を果たす。が、古典力学でもこれに似たような概念が
存在し、ポワソン括弧と呼ばれている。量子力学の定式化に悩んでいたDiracが、古典力学と量子力学との
間に密接な関連があることに気づいたのは、
ポワソン括弧をうろ覚えに覚えていたからであったことは有名である(このアイデアが閃いたとき、
Diracは日曜の散歩でケンブリッジ郊外の丘を歩いていたのであった)。
散歩から急いで駈けもどり、学生時代に習った解析力学の名著Whittakerの教科書を
図書館で確認しようとしたが、ケンブリッジ大学(St.John's college?)の図書館は日曜は閉館しており、
翌日の朝まで待ったという逸話も知られている。また、量子力学では、行列のみならず、線形代数そのものが
重要な役割を果たす。ベクトル空間は、無限次元のヒルベルト空間(内積が埋め込まれたベクトル空間)へと
拡張され、その空間に含まれる無限次元のベクトルとして波動関数が定義されるのである。
これもDiracの仕事である。
宿題に出した問題、「次の微分方程式を解け。
\[ \frac{dN(t)}{dt} = -N(t)\]
」には「誤り」がありました。もちろん、数学的にはこの微分方程式を解くことはできますが、
右辺と左辺で「次元」が合っていません。物理の微分方程式として捉えるなら、時間の次元を持つ
定数\(T\)を用いて
\[
\frac{dN(t)}{dt} = -\frac{N(t)}{T}
\]
と書くべきでした。
そこで新たなる宿題として、「\(T\)の物理的な意味を述べよ。また
半減期\(T_{1/2}\)とはどのような関係にあるか調べよ。」という問題を考えてみてください。
今週のテーマは微分と積分を自然科学に導入する、ということですが、そのためにまず
次の問いについて考えてみます。
物理の公式/定理と数学の公式/定理の違いはなにか?
授業では「三角形の内角の和が180度である」というユークッリド平面における定理
を例に議論しました。前提となる仮定、たとえばこの場合は「ユークリッド平面で」という
条件ですが、それがはっきりしている限り、数学の定理/公式は厳密に正しいものとみなして
適用します。一方で、物理の定理/公式に関しては、その「適用限界」について
気をつけながら使うことが多いと思います。自由空間中(つまりポテンシャルがない空間)
を慣性の法則にしたがって運動する質点mのエネルギーEは、果たして(いつでも)
\[
E=\frac{p^2}{2m} \quad \cdots \quad (1)
\]
と書けるのでしょうか?ただし、\(p\)は質点の運動量です。
物理では、複雑な形を持つ関数\(f(x)\)をべき級数で展開する、ということをよくやります。
べきとは\(x^k\)のように、ある変数xのベキ乗で表される量のことです。
ただし\(k\)は正の整数および0です。また、級数とは、ある無限列の和、
つまり無限和のことです。関数をべき級数で表す利点は、その解析的な扱いやすさにつきます。
微分も積分も簡単に実行できますし、連続性や収束性についても議論しやすいからです。
\(f(x)\)が無限回微分可能な場合、すなわち\(C^\infty\)級関数の場合、
べき級数はテイラー級数展開(あるいはマクローリン級数展開)によって表すことができます。
その上で、変数\(x\)の大きさに条件を適用することで、たとえば\(|x| \ll 1\)など、この
級数を「多項式近似」することができます。
例として、相対論的なエネルギーEと運動量pの関係式は\(E^2=(pc)^2 + (mc^2)^2\)
を考えてみます。エネルギーを運動量の関数だと思って表すと
\[
E= mc^2\sqrt{1+\left(\frac{p}{mc}\right)^2} \quad \cdots \quad (2)
\]
となりますが、この関数\(E(p)\)をマクローリン展開し、
\(p \ll mc\)という条件の下で多項式近似(\(p^2\)についての「線形」近似)を
行えば、非相対論的な(自由な)質点の運動エネルギー、すなわち式(1)が得られれます
(質量エネルギーの修正はつきますが)。
つまり、高校の物理で教わった「運動エネルギー」の式は、\(p\ll mc\)という「適用条件」の
中だけで成立する式だったのですが、あたかも「いつでも成り立つ式」、つまり数学の公式の
ように教わっていたということになります。大学で物理を学ぶときは、
高校の物理と異なり、「適用条件」とか「適用限界」について注意を払いながら
理論を組み立てたり、応用したりする必要が出てきます。これはとても重要なことです。
物理量Aを、別の物理量Bの変数とみなすとき、つまり\(A=A(B)\)、
AをBのベキ級数であ表せれば、分析が簡単になります。さらに、Bに条件をつけて、
この級数を多項式近似すると、もっと分析が簡単になります。これが、テイラー展開を
物理で採用する動機です。よく行うのが、線形近似、
\[
A(B) \simeq C_0 + C_1B,
\]そして放物近似
\[
A(B) \simeq C_0 + C_1 B + C_2 B^2
\]です。
数値計算など定量的な議論をする場合には、高次項を含む近似をする場合もありますが、
物理で重要な「定性的な議論」をするのには、放物近似くらいまでがちょうど良いのです。
たとえば、ケプラー問題(重力の2体問題)において、ケプラーの第三法則を簡単に
導く方法として、重力と「遠心力」の和、つまり有効ポテンシャルの安定点を見つけ出したあと、
その点の周りでテイラー展開の2次近似を行うという手法があります(微小振動近似)。
この講義でも、この計算は触れる予定です。
高校の物理で、振り子の問題などを扱うとき、\(\sin x \sim x\)と近似して良い、
という条件をよく目にしたと思いますが、これは正弦関数をマクローリン展開したときの
線形近似に相当します。より高次の項まで展開すると
\[
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots
\]
となります。\(|x|\ll 1\)とみなすと、線形近似してもjustifiedされるでしょう。
\(x\)がこの条件から外れ始めると、より高次の項を取り込む必要が出てくるかもしれません。
どの程度の近似にするのか、というのが「物理の感覚」と呼べるでしょう。
むやみやたらに精密計算するのもよくないし、みだりに線形近似するのもよくありません。
考えている物理の背景にもっとも適合するような「表現」を採用するのがよいのですが、
それができるようになると論文が書けるようになるでしょう。
さて、正弦関数のマクローリン展開には奇数のべきしか現れません。それはどうしてでしょうか?
次は積分についてですが、微分方程式を解くことが「積分」に相当します。
それがどうしてそうなのか、テイラー展開を利用して議論してみましょう。
講義では線形近似でまずやってみましたが、利点と同時に問題点も見つかりました。
次回の講義では、これを放物近似に拡張し、同様な「積分計算」をやってみる予定です。
力学の問題における目標とは、質点mの軌道\(\mathbf{r}(t)\)を得ることです。
この目標は運動方程式を解く、すなわち積分することで達成できます。
運動方程式を積分する方法は多種多様ですが、ここではTaylor(Maclaurin)展開を用いた
やり方をみてみます。
運動方程式は2階の微分方程式なので、その数学的な性質により初期条件2つが
パラメータとして残ります。物理では、このパラメータの決定に関しては、
「観測」によって決めるものと解釈します。ひとつめのパラメータは位置について、
2つめのパラメータは速度についての初期条件となります。それぞれを
定ベクトル\(\mathbf{r}_0,\mathbf{v}_0\)と表すことにします。
このベクトルは、「最初の時間」、つまり観測を始めた時間\(t_0\)、に測定した結果を表すものと
物理では解釈します(「初期条件」というのはそういう意味です)。
質点の軌道を知るということは、任意の時間t'において\(\mathbf{r}(t')\)の値を知る(計算する)
ということに他なりません。\(t'=t_0+\Delta t\)と解釈すれば、テイラー展開で\(t=t_0\)の
情報を元にt'における物理量を計算することが可能になります。すなわち
\[
\mathbf{r}(t') = \mathbf{r}(t_0+\Delta t) = \mathbf{r}(t_0) + \Delta t \frac{d\mathbf{r}(t_0)}{dt} + \frac{(\Delta t)^2}{2!}\frac{d^2\mathbf{r}(t_0)}{dt^2} + \cdots
\]
定義により\(\displaystyle\mathbf{r}(t_0)=\mathbf{r}_0, \frac{d\mathbf{r}(t_0)}{dt} = \mathbf{v}_0\)
と書けるので、上の展開は
\[
\mathbf{r}(t_0+\Delta t) = \mathbf{r}_0 + \mathbf{v}_0 \Delta t+ \frac{(\Delta t)^2}{2}\frac{d^2\mathbf{r}(t_0)}{dt^2} + \cdots
\]
と書けます。2次の項までみると、高校の物理で習った「定加速度運動の公式」に似ていることに
気づくでしょう。(これはどうしてなのか、高次の項はどうなるのか、などについては
各自考えてみてください。)\(\Delta t\)の値を満遍なく振って計算を繰り返せば、
原理的には任意の時間t'における位置ベクトルの値を計算することができ、軌道の情報を
(数値的に)得ることができます。ただし、そのためには無限次までの展開が必要になります。
現実的には、無限次の計算は不可能なので、\(\Delta t\)に制限を加えて、展開を多項式に近似して
計算することになります。よく行われるのが\(0<\Delta t \ll 1\)という条件を課し、展開項数を少数に抑える方法です。
最初に、線形近似(1次近似)でやってみましょう。
表記を簡単にするため、\(t_0=0, (\Delta t)^2 = \Delta t^2\)と書くことにします。
\[
\mathbf{r}(\Delta t) \simeq \mathbf{r}_0 + \mathbf{v}_0 \Delta t \quad \cdots (1) \quad , \\
\mathbf{v}(\Delta t) \simeq \mathbf{v}_0 + \frac{d\mathbf{v}(0)}{dt} \Delta t
= \mathbf{v}_0 + \mathbf{a}(0) \Delta t
\]
位置に関しては(近似の範囲内で)完全に決定されています(小学校で習った公式と同じもの)
が、速度に関しては加速度に関する初期情報\(\mathbf{a}(0)\)が指定されていない分だけ不定になっています。
力学では、加速度に関する情報は「運動方程式」で与えます。すなわち、
\(
m\mathbf{a} = \mathbf{F}
\)
です。力\(\mathbf{F}\)は、位置、速度、そして時間の関数とみなされます(それ以外の
力学変数に依存しないのはどうしてか考察してみてください)。仮に陽な(=explicit)時間依存性が
ないとすれば、
\[
\mathbf{F} = \mathbf{F}(\mathbf{r}(t), \mathbf{v}(t))
\]
と書けます。したがって、この場合、形式的には
\[
\mathbf{v}(\Delta t) \simeq \mathbf{v}_0 + \frac{1}{m}\mathbf{F}(\mathbf{r}_0,\mathbf{v}_0)\Delta t \quad \cdots (2) \quad
\]
と表すことができます。運動方程式が与えられ、力の形が明示的に与えられていれば
原理的には計算可能な量です。
ここでみたように、運動方程式の役割は、テイラー展開の高次の項を
0次、1次、そして2次の項に「書き戻す」ものとして理解することができます。
この側面については、またあとで詳細にみてみることにします。
\(\Delta t\)に置ける物理量が計算できたので、今度は\(2\Delta t\)に置ける計算をしてみます。
\[
\mathbf{r}(2\Delta t) \simeq \mathbf{r}(\Delta t) + \Delta t \frac{d\mathbf{r}(\Delta t)}{dt}
= \left(\mathbf{r}_0 + \mathbf{v}_0\Delta t\right) + \Delta t\left(\mathbf{v}_0 + \frac{1}{m}\mathbf{F}(\mathbf{r}_0,\mathbf{v}_0)\Delta t\right) \\
= \mathbf{r}_0 + \mathbf{v}_0 (2\Delta t) + O(\Delta t^2) \quad \cdots (3) \quad
\]
一方、速度ベクトルは
\[
\mathbf{v}(2\Delta t) \simeq \mathbf{v}(\Delta t) + \Delta t \frac{1}{m}\mathbf{F}(\mathbf{r}(\Delta t),\mathbf{v}(\Delta t)) \\
= \mathbf{v}_0 + \frac{\Delta t}{m}
\left(\mathbf{F}(\mathbf{r}_0,\mathbf{v}_0) + \mathbf{F}(\mathbf{r}_0 + \mathbf{v}_0\Delta t+\cdots, \mathbf{v}_0 + \frac{1}{m}\mathbf{F}(\mathbf{r}_0,\mathbf{v}_0)\Delta t + \cdots)\right)
\]
となりますが、力の寄与の部分を0次近似すると、全体として1次近似となり、
\[
\mathbf{v}(2\Delta t) \simeq \mathbf{v}_0 + \frac{2\Delta t}{m}\mathbf{F}(\mathbf{r}_0,\mathbf{v}_0) \quad \cdots (4) \quad
\]を得ます。
式(1)-(4)をみると一般に
\[
\mathbf{r}(n\Delta t) \simeq \mathbf{r}_0 + n\Delta t \ \mathbf{v}_0, \\
\mathbf{v}(n\Delta t) \simeq \mathbf{v}_0 + \frac{n\Delta t}{m}\mathbf{F}(\mathbf{r}_0,\mathbf{v}_0)
\]
が成立するように見えます。これは帰納法で証明できるでしょう。
ここで、線形代数を利用した理論を考えます。
さらに質点の運動が2次元平面に限られる特別な場合を考えます。
このような状況は、例えば中心力というタイプの力が作用する質点の運動にみられます。
重力や単振動に働く復元力が、このタイプの力です。
2次元平面において「一次独立」なベクトル、すなわち「基底」(あるいは基底ベクトル)
は2つあります(この性質の詳細は線形代数の教科書を参照してください)。
したがって、\(\mathbf{r}_0\)と\(\mathbf{v}_0\)が一次独立ならば、
この2つのベクトルを基底とみなし、
任意の2次元のベクトルを2つの基底の線形結合であらわすことが可能です。
すなわち
\[
\mathbf{F}(\mathbf{r}_0,\mathbf{v}_0) = C_0\mathbf{r}_0 + C_1\mathbf{v}_0
\]
と書けます(これは近似式ではありません)。
係数\(C_i\)は力の次元と一致するように決めます。
たとえば、減衰振動の場合は、\(C_0 = -m\omega^2, C_1 = -2m\gamma\)と
書くことができます。
そうすると、位置ベクトルと速度ベクトルをまとめて
\[
\left(\begin{array}{c}\mathbf{r}(n\Delta t) \\ \mathbf{v}(n\Delta t)\end{array}\right)
\simeq
\left(\begin{array}{cc}
1 & n\Delta t\\
C_0\frac{n\Delta t}{m} & 1+ C_1\frac{n\Delta t}{m}
\end{array}\right)
\left(\begin{array}{c}\mathbf{r}_0 \\ \mathbf{v}_0\end{array}\right)
\]
と表すことができます。
\(\Delta t\)の大きさをうまく選べば、任意の時間tにおける軌道が(線形近似で)
求まったことになります。すなわち
\[
\left(\begin{array}{c}\mathbf{r}(t) \\ \mathbf{v}(t)\end{array}\right)
\simeq
\left(\begin{array}{cc}
1 & t\\
C_0\frac{t}{m} & 1+ C_1\frac{t}{m}
\end{array}\right)
\left(\begin{array}{c}\mathbf{r}_0 \\ \mathbf{v}_0\end{array}\right)
\]
なにやらすごそうな関係式が出てきました。
しかし、力学の関係式により\(\mathbf{v}(t) = \dot{\mathbf{r}}(t)\)が成り立たねば
ならないので、\(C_0\)と\(C_1\)の関係式として
\[
C_0 \mathbf{r}_0 + C_1\mathbf{v}_0=\mathbf{0}
\]
が成り立たねばなりません。2つのベクトルが1次独立であるという
仮定により、\(C_0=C_1=0\)となり(線形代数の定理)、
結局、線形近似の場合は、得られた結論は「等速直線運動」という「当たり前の結果」
となってしまいました。
一般の場合に対し、この近似は明らかによくないことは、調和振動子などを考えれば
すぐにわかります。いくら近似とはいえ、軌道が「曲がる」効果が線形近似では
取りきれず、非物理的な結果になってしまったということです。
この問題を解決できる望みを託して、放物近似で同じ計算をしてみましょう。
果たして、もう少し物理的にまともな結果は得られるでしょうか?
前回の講義のあと質問がいくつか出ましたが、そのうちの2つについて考察してみたい
と思います。
(1) 斜交座標への変換をしたら、運動方程式はどのようになりますか?
(2) テイラー展開の2次近似で求めた結果を一般化し、厳密解を求めたら
\[
x(t) = \cos(\omega t) x(0) + \sin(\omega t) v(0) /\omega
\]
という2つの項の線形結合になったが、これは高校で習ったときの解と違うように見える。
高校の物理では余弦関数のみ(あるいは正弦関数のみ)で解を表したが、それと
今回求めた結果は整合性があるのでしょうか?
どちらも、線形代数の内容と関連があり、1次独立の概念や基底ベクトルと密接な関係が
あります。これらは、物理学では「(運動の)自由度」として解釈されます。
詳細は講義で議論します。
線形空間(ベクトル空間ともいう)についての説明:
質問(2)の解説の中で、線形空間について説明しました。
本来は数学の講義(線形代数とか解析とか)で教わる概念ですが、
物理でよく使う概念なので先取りして大枠のみ説明しました。
簡単なまとめをここに書いておきます。より「正しく」学ぶには、
佐武一郎著「線型代数学」(裳華房1958)のpp.86-103辺り、
などを参考にしたらよいでしょう。数学の教科書では「n次元ベクトル空間(\(V^n\))」というのを
最初から取り出して来ますが、我々は2次元に限定して考えることにします
(力学における運動方程式は2階線形微分方程式なので)。
ベクトル空間(線形空間)では、(1)ベクトル和と(2)スカラー倍の2つの演算が定義されています。
つまり、
\(\mathbf{A}=\lambda_1\mathbf{v}_1 + \lambda_2\mathbf{v}_2\)というタイプの演算の
ことです。(内積や外積は発展的な概念となります。)「演算が定義」されていると書きましたが、
この言葉の意味は、この演算によって生成された新しいベクトル\(\mathbf{A}\)が、
先にあたえられた2つのベクトル\(\mathbf{v}_1,\mathbf{v}_2\)が属するベクトル空間から
「飛び出していかない」ということです。言い換えれば、二次元ベクトル空間\(V^2\)
(これを平面Hと呼ぶことにする)に属する2つのベクトル\(\mathbf{v}_i\in V^2; i=1,2\)
の線形結合は、
再び\(V^2\)に属する二次元のベクトルとなるため(\(\mathbf{A}\in V^2\))、
平面Hから飛び出すような「3次元ベクトル」
などにはなり得ない、ということです。
\(\mathbf{v}_1\)と\(\mathbf{v}_2\)が一次独立な場合(「一次独立(線形独立ともいう)」
の数学的な定義は線形代数の講義や教科書で勉強しておいてください)、
いま考えている2次元ベクトル空間\(V^2\)
に含まれる任意のベクトル\(\mathbf{A}\in V^2\)は、
この線形独立なベクトルの組を使った線形結合によって
表すことが必ずできます。「線形独立」というのは、2次元の場合は「平行でない2つのベクトル」
と言い換えることもできます。
\[
\mathbf{A} = \lambda_1(\mathbf{A})\mathbf{v}_1 + \lambda_2(\mathbf{A})\mathbf{v}_2
\]
係数\(\lambda_i\)は\(\mathbf{A}\)に依存して変わりますから、\(\lambda_i(\mathbf{A})\)
と書きあらわしてあります。
高校の物理で、斜面を滑り降りる物体の運動を、斜面方向とそれに
鉛直な方向に分解して考えたのは、それぞれの方向を向いたベクトルが「線形独立」になっている
からです。斜面方向を\(\mathbf{v}_1\)とするなら、鉛直方向は\(\mathbf{v}_2\)となります。
\(\mathbf{A}\)を重力\(\mathbf{F}\)として考えるなら、
\(\lambda_i(\mathbf{F})\)は斜面の角度\(\theta\)を用いて\(mg\cos\theta\)とか
\(mg\sin\theta\)と書きあらわすことができることはご存知でしょう。
\(\mathbf{v}_1\)と\(\mathbf{v}_2\)が直交していると仮定すると、すなわち
\(\mathbf{v}_1\cdot\mathbf{v}_2=0\)、係数\(\lambda_i(\mathbf{A})\)は
次のように表せます。
\[
\lambda_i(\mathbf{A})= \frac{\mathbf{v}_i\cdot\mathbf{A}}{|\mathbf{v}_i|^2}
\quad \cdots\cdots \quad (1)
\]
どうしてこうなるかは簡単なので、自分で証明してみてください
(ちなみに、これは量子力学でもよく使う関係式です)。
一般のn次元ベクトル空間における線形独立なベクトルの最大数はnであり、これを
ベクトル空間の次元と言います。n個の独立なベクトルの組のことを「基底」といいますが、
n次元ベクトル空間を「テント」になぞらえるなら、基底ベクトルは、テントを支える屋台骨
とみなすことができるでしょう。3次元のテントなら屋台骨は3本、4次元のテントなら4本
が必要になるということです。
面白いことに、n階線形微分方程式の解に対しても、
「線形独立」の概念を適用することができます。これは大雑把にいうと、
微分方程式の解として得られた関数を「基底ベクトル」として取り扱うことができる、
という意味です(数学的な議論は数学の講義で確認しておいてください)。
前回の講義で扱った「1次元調和振動子」の問題における運動方程式は
\[
m\frac{d^2x(t)}{dt^2} = -m\omega^2x(t)
\]
という形でした。これは2階線形(同次)微分方程式というタイプの微分方程式です。
一般にn階の線形同次方程式の「線形独立な解」はn個あります。力学における
運動方程式は多くの場合、2階線形同次微分方程式というタイプの方程式と見なせますから、
線形独立な解の数は2つあります。調和振動子の場合は\(\cos(\omega t)\)と
\(\sin(\omega t)\)の2つだったのです。したがって、その一般階は正弦と余弦関数の
線形結合として書き表すことになったのです。さらにその係数が積分の未定係数に対応していた
というわけです。三角関数を「基底ベクトル」とみなし、その線形独立性をどのように定義するか、
という問題は、フーリエ理論(フーリエ級数理論やフーリエ変換理論)で取り扱うことになります。
フーリエ理論は、物理の枠内では、「振動波動」や量子力学の講義で議論されることになります。
今回の宿題は、デカルト座標で
\[
\mathbf{F}=\left(\begin{array}{c}F_x \\ F_y\end{array}\right)
\]
と表される2次元の力が、極座標ではどのように表されるか、という問題です。
より正確に書くと、極座標で\((F_r,F_\theta)\)と表され、デカルト座標で\((F_x,F_y)\)と
表される2次元の力\(\mathbf{F}\)の、異なる座標系における表現(デカルトと極座標)の間
の関係式を求めよ、という問題です。上で考えた式(1)と同じような方法で計算してみましょう。
まずデカルト座標の表現を、基底ベクトル\(\mathbf{e}_x,\mathbf{e}_y\)を使い、あえて
\[
\mathbf{F}=F_x\mathbf{e}_x + F_y\mathbf{e}_y
\]
と表します。極座標では異なる基底ベクトル\(\mathbf{e}_r,\mathbf{e}_\theta\)により、
\[
\mathbf{F} = F_r\mathbf{e}_r + F_\theta\mathbf{e}_\theta
\]
と書けます。ここで、基底ベクトルの性質を確認しておきます。デカルト座標系も極座標系も、
ともに「正規直交系」と呼ばれる基底です。つまり、
\[
\mathbf{e}_x\cdot\mathbf{e}_y = 0, \quad |\mathbf{e}_x|=|\mathbf{e}_y|=1,\\
\mathbf{e}_r\cdot\mathbf{e}_\theta = 0, \quad |\mathbf{e}_r|=|\mathbf{e}_\theta|=1
\]
を満たします。したがって、
\[
F_r = \mathbf{F}\cdot\mathbf{e}_r = F_x\mathbf{e}_x\cdot\mathbf{e}_r
+ F_y\mathbf{e}_y\cdot\mathbf{e}_r, \\
F_\theta = \mathbf{F}\cdot\mathbf{e}_\theta = F_x\mathbf{e}_x\cdot\mathbf{e}_\theta,
+ F_y\mathbf{e}_y\cdot\mathbf{e}_\theta \\
\]
となります。残りは、\(\mathbf{e}_x\cdot\mathbf{e}_r\)などの、いわゆる「変換行列」を
求めるだけです。もう少し詳しく見てますと、上の連立方程式は行列Tを使って、
\[
\left(\begin{array}{c}F_r \\ F_\theta\end{array}\right)
=
\left(\begin{array}{cc}
\mathbf{e}_x\cdot\mathbf{e}_r & \mathbf{e}_y\cdot\mathbf{e}_r \\
\mathbf{e}_x\cdot\mathbf{e}_\theta & \mathbf{e}_y\cdot\mathbf{e}_\theta
\end{array}\right)
\left(\begin{array}{c}F_x \\ F_y\end{array}\right)
\equiv
T
\left(\begin{array}{c}F_x \\ F_y\end{array}\right)
\]
と書けますが、極座標の基底がどのように表されるのか知らないとこの行列を決めることは
できません。戸田先生の教科書などを利用して調べ、変換行列Tが決まれば、
答えである\((F_x,F_y)\)と\((F_r,F_\theta)\)の間の関係式(それは線形関係になりますが)
を得ることができます。
極座標の応用問題として、円形の斜面を滑り落ちる質点の力学について議論しました。
講義中に考察したように、
斜面を滑り降りる力学の問題と比べて、この問題で「嫌な点」は、
場所によって「接線方向」や「垂直方向」が変わってしまうところです。
極座標というのは、場所場所で基底の向きが変わるような座標系ですから、
この問題に適した座標系であると言えます。
色々な座標の取り方があるとは思いますが、今回は図のような極座標およびそれに対応する
デカルト座標系を使います。
質点の位置\(\mathbf{r}\)は
\(
\mathbf{r}(t) = \left(\begin{array}{c} x(t) \\ y(t)\end{array}\right)
=a\left(\begin{array}{c} \cos\theta(t) \\ \sin\theta(t)\end{array}\right)
\)
であり、
\(t=0\)における初期条件は
\[
\mathbf{r}_0=a\left(\begin{array}{c} \cos\theta_0\\ \sin\theta_0\end{array}\right),
\quad \dot{\mathbf{r}}_0 =
a\dot{\theta}(0)\left(\begin{array}{c} -\sin\theta_0\\ \cos\theta_0\end{array}\right),
\quad \theta_0 \equiv \theta(0)
\]
とします。
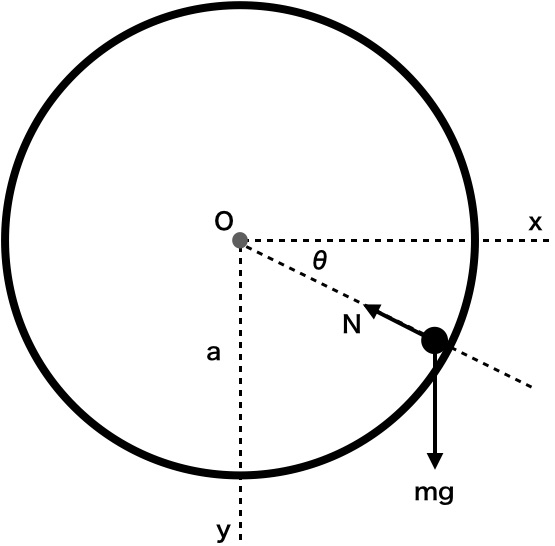
力は重力と垂直抗力であり、両者の合力をデカルト座標で表すと
\(\mathbf{F} = \left(\begin{array}{c}-N\cos\theta \\ -N\sin\theta + mg\end{array}\right)
\)と表すことができますが、前回の最後で得た「線形変換T」を用いて
\[
\left(\begin{array}{c}F_r\\ F_\theta\end{array}\right)
= T\left(\begin{array}{c}F_x\\ F_y\end{array}\right)
= \left(\begin{array}{c}-N+mg\sin\theta\\ mg\cos\theta\end{array}\right)
\]
を得ます(幾何学的に求めることもできます)。
本日の講義でまとめた、加速度\(\ddot{\mathbf{r}}(t)\)の(2次元)極座標表現を用いて
運動方程式を書き下すと
\[
m\left(\ddot{r}-r\dot{\theta}^2\right) = -N + mg\sin\theta\quad \cdots\cdots \quad (A),\\
\frac{1}{r}\frac{d}{dt}\left(mr^2\dot{\theta}\right) = mg\cos\theta \quad \cdots\cdots\quad (B)
\]
となります。拘束条件として\(r=a\)がありますから、\(\dot{r}=\ddot{r}=0\)となります。
これらを代入すると、
\[
\ddot{\theta} = \frac{g}{a}\cos\theta \quad \cdots\cdots \quad (1), \\
ma\dot{\theta}^2 + mg\sin\theta - N = 0 \quad \cdots\cdots \quad (2)
\]
を得ます。(2)式は、高校の物理で習った「円運動の釣り合いの式」に相当するものです。
この式の左辺第1項が「遠心力」であることはすぐにわかるでしょう。
(1)式が実質的な運動方程式です。
この問題は2次元の問題という設定ですが、拘束条件があるため、
有効な自由度(力学変数)が角度\(\theta\)のみの、実質1次元運動です。
この微分方程式の解は初等関数で表すことはできませんが、
特殊関数の一つである(Jacobiの)楕円関数を使って表すことができます。
楕円関数の説明はまた後で議論することにして、ここでは\(\theta=\frac{\pi}{2}\)
周りの微少振動を考えることにします。
初期条件として\(\theta_0=\frac{\pi}{2}-\Delta\theta_0\), \(|\Delta\theta_0|\ll 1\)とし、
\(\theta=\frac{\pi}{2}\)の周りの微少振動を考えます。テイラー展開を用いると、(1)式は
次のような微分方程式に近似することができます
(微少振動を記述するため、力学変数を\(\theta\rightarrow \frac{\pi}{2}-\Delta\theta\)と
書き直します。が、見やすくするために、以下では\(\Delta\theta\equiv \phi\)と
書くことにします)。
\[
\ddot{\phi} = -\frac{g}{a}\phi
\]
以前の講義でやったように、テイラー展開を利用してこの運動方程式を解くことができます。
たとえば、
\[
\phi(\Delta t) = \phi(0) + \Delta t\dot{\phi}(0) + \frac{\Delta t^2}{2}\ddot{\phi}(0)
+ \cdots \\
= \phi_0 + \dot{\theta}_0 \Delta t + \left(-\frac{g}{a}\phi_0\right)\frac{\Delta t^2}{2} + \left(-\frac{g}{a}\dot{\phi}_0\right)\frac{\Delta t^3}{3!} + \cdots\cdots \\
=\phi_0\left(1 - \frac{g}{a}\frac{\Delta t^2}{2!} + \cdots\right)
+ \dot{\phi}_0\left(\Delta t - \frac{g}{a}\frac{\Delta t^3}{3!}+\cdots\right)
\\
= \phi_0 \cos(\omega\Delta t) + \frac{\dot{\phi}_0}{\omega}\sin(\omega\Delta t),
\]
という具合に解くことができます。ただし\(\omega = \sqrt{\frac{g}{a}}\)としました。
もちろん、この解は調和振動子の解です。テイラー展開などの数理手法を用いて、
物理の問題をわざわざ近似する目的の一つは、「解ける形」に近づけることにあります。
ここでもう一つ重要なのは、解の中に、積分定数として初期値\((\phi_0, \dot{\phi}_0)\)の2つが
含まれているということです。この2つの量は、物理における「観測量」に対応しますので、
数理的な手法を用いて決めることはできません。
解を特定するためには2つの観測量(すなわち積分定数)が必要であるという事実は、
運動方程式が2階線形微分方程式であることの反映です。
[回転に関する議論]
先週と今週の講義では、\((F_x,F_y)\)という表現(デカルト座標)と
\((F_r,F_\theta)\)という表現(極座標)との間に、線形関係が成り立つことを議論しました。
この関係式は、変換行列Tで表せるわけですが、講義で計算してみたように、
Tは回転行列Rとなります。
\[
T=R(-\theta) = \left(\begin{array}{cc}\cos\theta & \sin\theta \\ -\sin\theta & \cos\theta
\end{array}\right)
\]
一般に、正方行列\(A\)の逆行列\(A^{-1}\)は、単位行列\(I\)を用いて
\[
AA^{-1}=A^{-1}A = I
\]
を満たす行列であると定義されます。この定義から2次元の正方行列の場合には
逆行列の公式を簡単に導出することができます。以上より、回転行列の逆行列は次のような
性質を持っていることが示せます。
\[
R(\theta)^{-1} = R(-\theta)
\]
すなわち、力の関係式は
\[
\mathbf{F}_{\rm cartesian} = R(\theta)^{-1}\mathbf{F}_{\rm polar},
\]
あるいは逆変換を考えて
\[
\mathbf{F}_{\rm polar} = R(\theta)\mathbf{F}_{\rm cartesian} \quad\cdots\cdots\quad (3)
\]
と表すことができます。「回転変換」Rは、ベクトルFを「動かす機械(クランク)」
みたいなものと、物理的には解釈します。
この関係式(すなわちRが回転を意味するということ)をもう少し直感的にわかりやすくするには
複素平面を使った考えが役立つでしょう。すなわち\((F_x,F_y)\)というデカルト座標風の
2次元表現を、複素数\(\mathcal{F}\)を用いて\(\mathcal{F}=F_x + iF_y\)と
1次元的に表します。極座標風に
\[
F^2 = F_x^2 + F_y^2, \quad \tan\theta = \frac{F_y}{F_x}
\]
というように変数(F,θ)を導入すると、
\[
\mathcal{F} = F\left(\cos\theta + i \sin\theta\right)=F{\rm e}^{i\theta}
\]
と書くことができます。最後のところではオイラーの公式
\[
{\rm e}^{i\theta} = \cos\theta + i\sin\theta
\]
を用いています(この公式の簡単な証明にもテイラー展開が役立ちます)。
回転した後、複素表示した力が\(\mathcal{F}'=F_x'+iF_y'\)になったとします。
回転に対してベクトルの大きさ(ノルム)は変わりません(\(F=F')\)。方向だけが変わります。
回転前の力は\(\theta\)の方向を向いていましたが、回転後の力は\(\theta+\phi\)の
方向を向いていると仮定します。そうすると、上で見たように
\(
\mathcal{F}'=F{\rm e}^{i(\theta+\phi)}
\)
と表現できます。これを次のように書き換えます。
\[
\mathcal{F}'={\rm e}^{i\phi}\left(F{\rm e}^{i\phi}\right) = {\rm e}^{i\phi}\mathcal{F}
\quad\cdots\cdots\quad (4)
\]
この(4)式は、上で得た行列を用いた(3)式と同じような形になっていることに気づくでしょう。
この場合は「クランク(回転機械)」とみなせるのは、複素数\({\rm e}^{i\phi}\)です
(位相因子ともいいます)。(4)式を次のように成分で書き下し、実数部と虚数部でまとめると、
(3)式が得られますから、2つの式は数学的に同値です。
\[
F_x'+iF_y' = \left(\cos\phi + i\sin\phi\right)(F_x+iF_y) \\
= (\cos\phi F_x - \sin\phi F_y) + i(\sin\phi F_x + \cos\phi F_y)
\]
[宿題]2次元の正方行列の逆行列を計算してみてください。また、それを
回転行列に当てはめると、回転行列が直交行列であることがわかりますので、
確認してみてください。
[本日の質問] 講義の後に質問がいくつか出ましたが、そのうちの一つについてここで
言及しておきます。質問は「教科書では\(F_\theta=0\)としてある方程式が書いてあるが、
どうして講義ではそうなっていないのか」というものでした。彼の教科書をみると、上の式(B)に
対応する運動方程式が
\[
\frac{d}{dt}\left(mr^2\dot{\theta}\right) = 0
\]
と書いてありました。我々の講義で扱った問題では\(F_\theta=mg\cos\theta\)であり、
これが実質的な運動方程式(1)になったわけです。見せてもらった教科書のように
もし\(F_\theta=0\)となるとしたら運動方程式は出てきませんからまずい状況になりますね
(そのかわり保存則がでます)。これはどういうことでしょうか?答えは、教科書が扱っていたのは
「中心力」という特別な場合だったからです。中心力の例としては万有引力(一般の重力問題)
があります。重力の問題(ケプラー問題ともいう)は後半(第7-8回あたり)で議論しますから、
もう少し待っていてください。
様々な保存則について考察しました。
まずは、1次元調和振動子の運動方程式(質量の時間変化がないとする)
\[
m\ddot{x}(t) = -m\omega^2x(t)
\]
を用いたエネルギー保存則について。
ばね定数\(k\)は\(k=m\omega^2\)という関係により定義されます。
両辺に\(\dot{x}(t)=dx(t)/dt\)をかけると
\[
\frac{d}{dt}\left(\frac{1}{2}m\dot{x}^2 + \frac{1}{2}m\omega^2x^2\right)=0
\]
となります。これを積分したものが「エネルギー積分」です。
このときの積分定数Eが力学的エネルギーに相当するものになります。
つまり、上の式は「(力学的)エネルギー保存則」を意味します。
次に運動量保存則を考察しました。
この保存則は、運動方程式\(\displaystyle \frac{d\mathbf{p}}{dt}=\mathbf{F}\)に対して、
\(\mathbf{F}=\mathbf{0}\)が適用される特別な場合に成立します。
すなわち、運動量の保存則は
\[
\frac{d\mathbf{p}}{dt}=\mathbf{0}
\]
という式で表されます。質点の一体問題について考えると、「慣性の法則」の
数学的表現とみなすことができますが、運動量保存則がもっとも効力を発揮するのは
外力が働かない孤立多体系の力学です。重心とか、相対運動とかいう概念が登場します。
このテーマについては、別の機会にもう少し丁寧に議論する予定です。
最後に、角運動量保存則を見ました。
これは本日の講義で触れた「中心力」の場合に成立する保存則で、
角運動量という物理量が保存します。
中心力とは、2つの質点の間に作用する力が、質点同士を結ぶ直線方向にのみ働くような力です。
一つの質点を原点におき、もう一つを点\(P(x,y)\)に置いたとき、この2つの質点に働く
中心力の一般形は
\[
\mathbf{F} = f(r)\mathbf{e}_r=\frac{f(r)}{r}\mathbf{r}
\]
と表されます(\(\mathbf{e}_\theta\)成分がないのが重要です)。
本来角運動量という量は3次元空間で定義される量ですが、2次元空間の場合でも
対応する量(ケプラーが見つけた面積速度)があります。運動方程式を2次元極座標で
書き直した時、中心力の定義により\(F_\theta=0\)となりますから
\[
\frac{d}{dt}\left(mr^2\dot{\theta}\right)=0
\]
という式が「角運動量保存則」に相当する式(ケプラーの第二法則に対応)となります。
前回の講義で出た質問はこの保存則に関連するものでした。
ケプラー問題についての議論も行いました。高校の物理でのアプローチ、ファインマン物理に
のっている「りんごに働く重力」と「月に働く重力」は同じものか?という問題、
そして中心力としての万有引力を極座標表示の運動方程式に応用した場合、について考察しました。
最後のテーマについては、来週の講義でも続きの議論を行います。
[宿題] 中心力に従って運動する質点は、それが3次元空間中にあったとしても、
その中の2次元平面中の運動に拘束されることを証明せよ。
中心力の条件\(F_\theta=0\)を使って、動径方向の運動方程式を書き下すと
\[
m\ddot{r} - \frac{L_0^2}{mr^3} = -m\frac{GM}{r^2}
\]
となります。左辺が「本当の加速度」、右辺が「本当の力」と解釈します(当然ながら)。
一方で、左辺第二項を右辺に移行すると
\[
m\ddot{r} = -m\frac{GM}{r^2} + \frac{L_0^2}{mr^3}
\]
となりますが、これは1次元の運動方程式と(形式的に)解釈することができます。
つまり、この書き直した式の左辺を「形式的な加速度」とみなし、右辺を「形式的な力」
(あるいは「有効力」)と解釈するわけです。
今考えている2次元極座標系問題の場合、移行した式は遠心力に相当するものですが、
一般の場合でも、本当の加速度の一部の項(例えばコリオリ項など)を移行して、
非慣性系に現れる見かけの力、すなわち慣性力と呼ばれるものとして理解することが可能です。
このあたりの説明は、回転座標系における運動方程式の議論で再考します。
一般相対論でもこのような考え方(慣性系と非慣性系の対応)は重要になりますので、
頭の隅にちょっとだけでも入れておくとあとで楽になります。
この微分方程式は非線形なので、「これさえやればうまくいく」
といった一般的な解法はありません。数学的にどう解くか大きな問題です。
多くの教科書では\(r=r(t)\)の形の解を得ることは「困難」だと解説しています。
時間の関数としての軌道情報を得るという目的に「近づける」目的で
ケプラー方程式という形に書き直す方法もありますが、天文学に進む学生以外は
これに習熟してもあまりご利益はないかもしれません(数値計算のよい練習になったり、
ベッセル関数やフーリエ級数展開の練習問題とみなすことは可能かもしれませんが)。
ケプラーの第一法則を確認するだけなら、\(r(t)\)の形を陽に求める必要はなくて、
焦点の周りの角度\(\theta\)の関数として軌道を求める、つまり\(r=r(\theta)\)を
運動方程式から導くだけですみます。とはいえ、この導出もnon-trivialな変形をいくつか
行なった末に可能になります。ほとんどの教科書では、この導出について詳細な説明が
与えられていますので、余力のある人はぜひ自習してみてください。
ここでは、運動方程式のエネルギー積分を行い、そこで得られる(有効)ポテンシャルエネルギー
\(V(r)\)の停留点周りの微少振動を考えます。これは停留点付近におけるテイラー展開の2次近似に
相当します。この近似で得られた運動方程式は、停留点周りの調和振動子を記述する
(1次元)微分方程式となりますので、私たちは積分することができます。
このように、難しい問題を、特別な場合に(漸近形とか、微少振動など)限定して近似し、
解析的によくわかっている問題に書き直すという方法は物理学ではよく使われる手法です。
この手法の発展形として、摂動展開という方法があります。例えば、ファインマンらによる
量子電磁力学(QED)の完成形はこの手法(摂動展開)とくりこみの手法により
綺麗に表現することができます。
[宿題] 歴史的には、逆2乗則に従う質点に対する運動方程式を解いて、
楕円軌道やその他のケプラーの法則を導出したのではなく、その逆、つまりケプラーの法則が
先に見つかって、その法則を満たすような「作用」は何か?という問題の解として、
逆二乗則が発見されたという経緯があります。山本義隆氏[Ya97]
によれば、前者が「逆問題」、後者が「順問題」とみなされます。今週の宿題は、
順問題を解いて、楕円の方程式から逆二乗則を導出することにします。このためには、
高校で習った楕円の方程式
\[
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\]
を、極座標に似た表現
\[
r(\theta)= \frac{F}{1+\epsilon\cos\theta}
\]
に書き直す必要があります。ただし、\(\epsilon = a/f, f=\sqrt{a^2-b^2},
F= f(1-\epsilon^2)/\epsilon\)という関係があります。\(\epsilon\)を離心率、
\(f\)を焦点の位置ということもあります。また、\(a>b\)を仮定してあります。
演習問題として、講義中にみんなで計算してみましたがかなり手こずりました。
どうすれば一番うまく計算が進むか研究して見てください。
物理の研究では、時に代数計算の効率性の研究も必要になるのです(良い例が
Feynmanの教科書[FeGd15]の冒頭部分に載っています)。
またWolframのように、代数計算を効率よく行うアルゴリズムを開発し、それをソフトウェアとして
開発できれば(つまりMathematicaのようなもの)、一攫千金の可能性もあるでしょう。
本日の講義では、シュレディンガーの「生命とはなにか」を読むための最初の関門である
「なぜ生命体は古典力学が適用できる大きさなのか」という問題について議論しました。
そのためには、量子力学の二重スリットの問題を少しだけ理解する必要があります。
ファインマンの教科書に従い、銃弾の場合と、波の場合について考え、電子がどちらに近いか
検討しました。日立中央研究所の外村さんの有名な実験は、
こちらのページから閲覧することができます。
銃弾の軌道に関しては「力学」の範疇ですから、
(慣性の法則がなりたつような単純な状況を考えれば)
どちらかの穴の後ろに着弾することになります。
波動の場合は、高校でやった「ホイヘンスの原理」にしたがえば、干渉縞が生じることは
ご存知でしょう。電子は素粒子ですが、日立の実験のように干渉縞を生じますので、
波動とみなすべきなのでしょうか?この問は量子力学を勉強すると得られますが、ここでは
そうではなくて、生命体との関わり合いで考えてみましょう。
毛細血管が二手に別れるとき、赤血球がどちらの経路を選ぶか考えみます。
もし、赤血球が電子と同様の大きさで、毛細血管の枝分かれのサイズが
量子力学が適用できるようなサイズだったとしたらなにが起きるでしょうか?
赤血球の運動は古典力学の運動方程式にしたがうべきだとすれば、銃弾のように
古典力学に従うようなサイズでないといけません。シュレディンガーはこのような
生命の物理機能に関して考察し、生命体のサイズがどうしてこの大きさなのか議論しています。
もし、量子力学に従うようなサイズの世界最小(宇宙最小?)の生命体が発見されたら、
おそらくノーベル賞が与えられるでしょう。
「楕円の方程式を極座標で考えるとき、なぜ焦点の周りに設定するのか?」
という質問に対する考察:
この質問に対する答えは一言で言うと「ケプラーがそうしろといっているから」ということに
なりますが、もう少し丁寧に見てみましょう。
講義の中では、原点(つまり楕円の中心)周りの極座標で楕円の方程式を導いてみました。
まずはその計算の概略をまとめておきます。楕円上の点(x,y)をこの極座標で表すと
\[
\left(\begin{array}{c}x \\ y\end{array}\right) =
\left(\begin{array}{c}r\cos\theta \\ r\sin\theta\end{array}\right)
\]
となりますので、これを楕円の方程式\(x^2/a^2 + y^2/b^2 = 1\)に代入すると、
\[
r^2\left(\frac{\cos^2\theta}{a^2} + \frac{\sin^2\theta}{b^2}\right) = 1
\]
を得ます。次に\(\sin\theta\)を消去し、\(a,b\)を\(f,\epsilon\)で書き直します。
\[
\left(\frac{1}{a^2}-\frac{1}{b^2}\right)\cos^2\theta + \frac{1}{b^2} = \frac{1}{r^2}
\quad \rightarrow \quad
r^2 = \frac{f^2(1-\epsilon^2)}{\epsilon^2} \frac{1}{1+\epsilon^2\cos^2\theta}
\]
したがって、原点周りの極座標による楕円の方程式は
\[
r = \frac{f\sqrt{1-\epsilon^2}}{\epsilon}\frac{1}{\sqrt{1+\epsilon^2\cos^2\theta}}
\]
となりました。これは初めてみる楕円の方程式です(少なくとも、どんな力学の教科書にも、
この表式は載ってないでしょう)。ここまでの考察で十分ならば、
ちょっとした「発見」のような気分になりますが、この先に進むことを考えると、
分母に現れた平方根が嫌な感じを与えます...
戸田先生の教科書[Td82]のように逆数を取ってから微分してみましょう。
\[
-\frac{\dot{r}}{r^2} = \frac{\epsilon}{f\sqrt{1-\epsilon^2}}
\frac{1}{2}\frac{1}{\sqrt{1+\epsilon^2\cos^2\theta}}
2\epsilon^2\cos\theta(-\sin\theta)\dot{\theta}
\]
平方根の部分は\(r\)と置き換えられそうな感じがしますが、\(\cos\theta\)の2次式が
あるせいで、微分すると\(\sin\theta\)が出てきてうまくありません。
また、面積速度の保存則をつかって\(\dot{\theta}\)を消去したいのですが、
ケプラーによれば、面積速度でかんがえる面積は「焦点」の周りの面積なので、この極座標では
うまく表現できないのでやはりうまくいきません。
やはり、面積速度で現れる「角度座標」は焦点周りの角度であることを納得するには、
「逆問題」を解いておく必要があるのかもしれません。「逆問題」の解き方は、
色々な教科書に載っています(戸田先生の本を含む)ので、興味のある人は研究してみてください。
[レポート課題: 締め切りは6月20日]
- ケプラー問題の微少振動近似
- 1次元調和振動子の運動方程式の解法(選択)
- 中心力の運動が2次元平面に拘束されることの証明(選択)
進化論において"convergent evolution"(「収斂進化」?)という概念がありますが、
これは違う種であっても環境に適応するために同じような形態を獲得する性質を
(地球上の)生物はもっているようです。私が知っている例は哺乳類であるイルカと
爬虫類であるイクチオサウルスです(Wikipediaには魚類のサメと鳥類のペンギンも
加えられていましたが、後者に関しては少し苦しいのではと個人的には思います)。
これと同じようなことが力学と電磁気学の方程式にも存在します。
(1次元)減衰振動とLCR回路です。
|
\[ m\frac{d^2}{dt^2}x(t) + 2m\gamma\frac{d}{dt}x(t) + m\omega^2x(t) = 0\]
|
\[ L\frac{d^2}{dt}Q(t) + R\frac{d}{dt}Q(t) + \frac{1}{C}Q(t) = 0\]
|
| 1次元の減衰振動の運動方程式 |
LCR回路の電圧降下(キルヒホッフの定理を適用した)の微分方程式 |
したがって、減衰振動の解はLCR回路の解としても再利用できるということになります。
このタイプの微分方程式を解く方法はいろいろあるでしょうが、もっとも簡単に解くには
"Ansatz法"がよいでしょう。(ただし、Ansatz法はいつでも使える方法というわけではないので、
注意が必要です。)この問題では\(x(t) = C\exp(\lambda t)\)という具合にAnsatzを設定すると、
微分方程式を代数方程式(しかも二次方程式)に帰着させることができ、
簡単に解くことができます。
講義では、失敗する例(たとえばテイラー展開による方法やプランクの放射公式で利用されたような
2つの漸近形を結ぶような手法)に関しても議論してみました。実際の研究では
ひとつの方法だけでいつもうまく行くわけではないので、失敗を気にせず色々な手法を試してみる
のが肝要です。
Aセメスターで受講する予定になっている電磁気学に繋がる内容として、
3次元空間中のエネルギー保存則について講義しました。
出発点は、直感的にもわかりやすい「仕事」の定義からです。この物理量は「エネルギー」の
次元を持っていますので、最終的にはより抽象的な「エネルギー」、そしてその保存則の
導出へとつながっていきます。高校の物理(物理基礎?)では仕事\(W\)は、力\(F\)と
移動距離\(x\)により, \(W=Fx\)と定義されました。
しかしこれでは直線上の仕事しか計算できません。曲線Cに沿った仕事を計算するには、
まず曲線を細分し、無数の短い直線で近似します。短い直線における微小仕事\(d'W\)は
\(d'W=F(x)dx\)と書けます。3次元空間では、力も位置もベクトル情報で表されますから、
これを\(d'W=\mathbf{F}\cdot d\mathbf{x}\)と拡張します。したがって、
曲線Cに沿った全仕事の量は
\[
W=\int_{C}\mathbf{F}\cdot d\mathbf{x}
\]
と積分によって表すことができます。このようなタイプの積分を線積分といいます。
つまり、3次元空間の力学では、「仕事」を線積分によって定義します。
質量が時間変化しないような質点を考え、その質点に対する運動方程式
\(\displaystyle \mathbf{F} = \frac{d\mathbf{p}(t)}{dt}=m\frac{d\mathbf{v}}{dt}\)を、
線積分に代入すると
\[
W = m\int_{C}\frac{d\mathbf{v}}{dt}\cdot d\mathbf{x}
= m\int_{t_0}^{t_1}\frac{d\mathbf{v}}{dt}\cdot \frac{d\mathbf{x}}{dt} dt
\]
となります。最後の等式の部分では変数変換を導入して、線積分を時間をパラメータとする
1次元パラメータ積分へ書き直しています。速度は位置ベクトルの1階微分で表されることを
利用すると、この積分は
\[
W= m\int_{t_0}^{t_1} \frac{d}{dt}\left(\frac{\mathbf{v}^2}{2}\right) dt
= \left(\frac{1}{2}mv^2\right)_1 - \left(\frac{1}{2}mv^2\right)_0
\]
となって、曲線Cの端点における運動エネルギーの差となります。
つまり積分結果が、曲線Cの経緯によらず、その端点のみの情報で決まるということです。
この性質はとても重要で、このあと「ポテンシャル」を導入する際に効いてきます。
積分経路によらず、積分値が一定に定まるということは
\[
\int_C \mathbf{F}\cdot d\mathbf{x} = \int_{C'} \mathbf{F}\cdot d\mathbf{x}
\]
ということです。CとC'は端点は同じですが、異なる経路を表す記号とします。
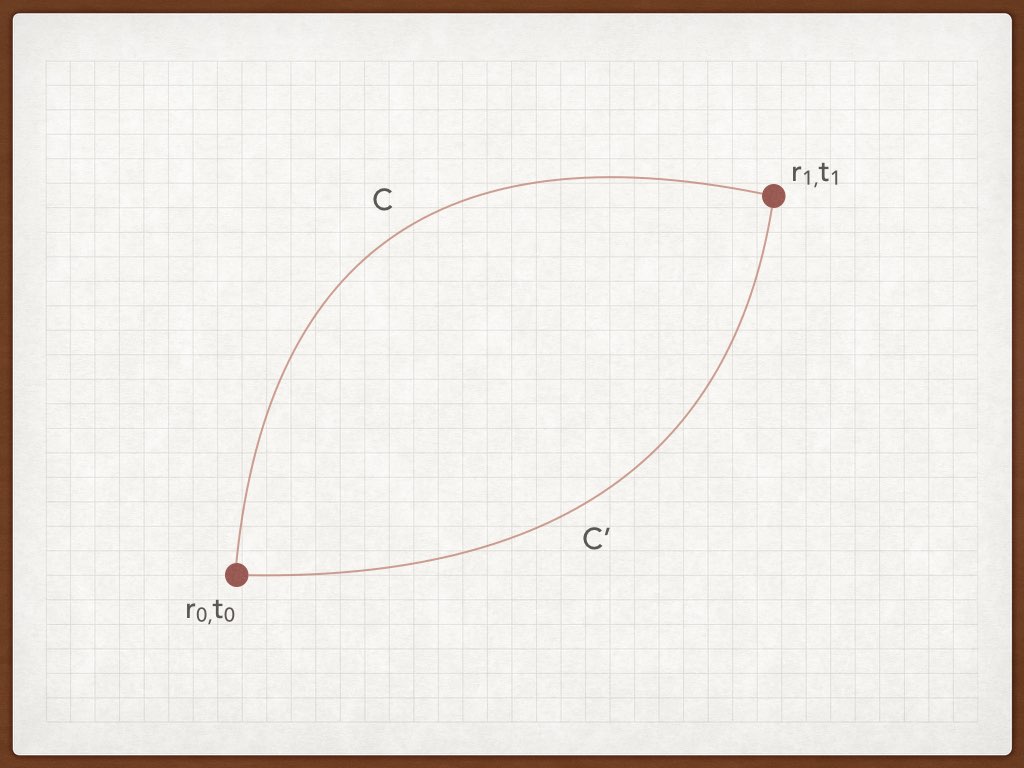
この等式は
\[
\int_C \mathbf{F}\cdot d\mathbf{x} - \int_{C'} \mathbf{F}\cdot d\mathbf{x} = 0.
\]
と書き直すことができます。
右辺を左辺に移行すると負号がつきますが、これは積分経路の向きを「反転」させることに
対応します。高校数学でも
\[
\int_a^b f(x)dx = -\int_b^af(x)dx
\]
という恒等式を習ったと思いますが、それに相当するものです。
線積分では\(C\rightarrow -C\)という記号で、この「反転」を表すことがあります。
すなわち
\[
\int_C \mathbf{F}\cdot d\mathbf{x} + \int_{-C'} \mathbf{F}\cdot d\mathbf{x} = 0.
\]
この2つの積分の和は、結局\(\mathcal{C}=C-C'\)という「ループ」に沿って
積分をすることを意味します。したがって、
\[
\oint_{\mathcal{C}} \mathbf{F}\cdot d\mathbf{x} = 0
\]
となります。左辺のような線積分を「周回積分」あるいは「ループ積分」といいます。
つまり、線積分の値が経路によらない、という条件は、周回積分が零値をとる、ということと
同値です。
通常は電磁気学で習うと思いますが、ここで周回積分と「面積分」を結びつける「ストークス
の定理」という定理を利用して、上式を書き直して見ます。ストークスの定理は
\[
\oint_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{x} =
\int\int_{S} \left(\mathbf{\nabla}\times\mathbf{F}\right)\cdot\mathbf{n}dS
\]
と表されます。面積分についての詳細は
夏休み中に電磁気の教科書などを利用して予習してみてください。
この定理を利用すると、周回積分が零値をとる、という条件は、
「力場\(\mathbf{F}\)」の循環\(\mathbf{\nabla}\times\mathbf{F}\)が零値をとる、
という条件と等価であることがわかります。つまり
\[
\mathbf{\nabla}\times\mathbf{F} = \mathbf{0}
\]
が成立します。ベクトル場の循環という概念が新しく出てきましたが、これも
電磁気などで通常は最初に習う概念です。電磁気の教科書で予習しておいてください。
ベクトル解析の定理で、循環が零値をとるようなベクトル場はスカラー場\(U\)の
勾配(これもベクトル解析の概念です)で表せることが知られています。つまり、
\[
\mathbf{F} = -\mathbf{\nabla}U(\mathbf{x})
\]
です。右辺の負号は「物理的な考察」によって付されています(数学的には+でも
構いませんが、どうして物理的には負号が付されるのか考えてみてください)。
ここで導入されたスカラー場\(U\)がポテンシャルエネルギーに相当するものです。
このように定義される力は、(端点が共通ならば)経路によらず同じ仕事を与え、
「保存力」と呼ばれます。「非保存力」の例としては、減衰振動に現れた「速度に依存する力」、
つまり抵抗/摩擦に相当する力があります。
2017年度Sセメスター(水曜日4限)開講:理科I類(33,34,35組)
このページの目次
- 教科書/参考書
- はじめに
-
[第1回]
調和振動子をつかった、数学と物理の関連性
-
[第2回]
調和振動子とマクローリン展開
-
[第3回]
調和振動子と代数的手法
-
[第4回]
強制振動と線形性
-
[第5回]
エネルギー積分とポテンシャル
-
[第6回]
振り子の問題と二次元調和振動子
-
[第7回]
慣性の法則と向心力
-
[第8回]
二次元調和振動子(2)デカルト座標と極座標
-
[第9回]
二次元調和振動子(3)中心力、動径方程式、角運動量
-
[第10回]
ケプラー問題と重力(万有引力)
-
[第11回]
微少振動近似、角運動量
-
[第12回]
2次元回転と2体問題
教科書: 戸田盛和
(岩波書店1982年、物理テキストシリーズ4)[Td82]
自習の際の「案内図」として使用してほしい。
教科書の詳細をひたすら覚えるということではなく、
教科書の行間を読みとり、教科書の先にあることに気付けるようになりたいものである。
(結局、教科書にないことを見つけるのが「研究」である。)
戸田先生の教科書は、大学初年度に学ぶべき力学の要点が網羅されていて、
「案内図」にはもってこいの内容である。この本を出発点として、下記の色々な参考書に
あたりながら、様々な観点から力学の理論をじっくり学ぶことが、
意外にも現代物理学や最先端の科学分野へ到達する「近道」になっているような気がする。
(しかし、この教科書にはひとつ問題がある。それは調和振動子についての議論が少ないこと。
摩擦/抵抗力のある場合や強制振動などの議論も含まれていない。
可解な非線形力学模型である「戸田格子」を生み出した戸田先生が、
ご自身の教科書で調和振動子についてあまり議論していないのは、ある意味興味深い。
これは、量子電気力学を編み出したファインマンが、初年度向けの教科書ですら、
グリーン関数だの、経路積分だの、最小作用の原理だの、非保存力はない(原子間の
電磁相互作用を考えれば)だの、自分の得意/専門分野をふんだんに盛り込んだ書き方とは
非常に対照的である。)
ちなみに、現在(Apr. 5, 2017)、駒場の博物館で、
戸田先生の生誕100周年記念展が開催されていて、先生の遺品を拝見することが
できる。ファインマン物理学の4巻は戸田先生の訳であり、その縁で、
おそらくファインマンが来日した
際に、戸田先生のお宅に遊びにいったのであろう。そのときの、墨筆による悪戯書き
(とっていも、Dirac方程式と、量子力学の交換関係のなぐり書き)が展示されている。
参考書:
-
「ファインマン物理学:力学」ファインマン、レイトン、サンズ著[坪井忠二訳]
(
岩波書店)[Fe69]
カリフォルニア工科大学(CalTech)で教鞭をとっていた、ファインマン教授の
講義をもとに編集し作成した教科書。講義は難しすぎて
脱落者続出、しかもせっかく作ったこの教科書も物理教育には不適ということになり、
早々とCalTechの標準教科書指定から外されてしまったという。
にもかかわらず、いまだに、この教科書は、
物理を学ぶ学生、物理を研究する物理学者に、世界中で読み継がれている名著である。
矛盾する2つの評価を得たこの本の特徴は、(i)ファインマンが展開する
独特の物理観は、標準的な物理教育課程とはかなり異なっている
(ii)現代の力学の学習項目と比較して、項目が系統的に提示されていない。
(iii)相対論的力学がさっそく登場するなど、発展的な内容への展開が早い
(iv)古典力学なのに、統計力学や量子力学で学ぶべき原子論的な観点が
提示される、などなどがある。
上に掲げた、この本の「良い点」は、大学で物理を初めて学ぶ学生たちにとっては
「悪い点」でもありうる。そこがこの本の難しさであり、面白さでもある。
原著では、力学、光学、熱力学あたりまでを包括的にまとめた内容が第一巻と
なっているが、和訳では、力学とそれ以外が切り離されて、一巻と二巻とに
分離されている。力学Aでは一巻の内容だけしか教えないが、二巻の方が面白いので
ぜひ読んでみてもらいたい。特に、フェルマーの最小時間の原理の解説で
用いられる、海で溺れる人をみつけた救助隊員がとるべき
経路に関する例は傑作ではないだろうか?
「物理学序論としての力学」藤原邦男著
(
東大出版会)
[Fj84]
駒場で長らく教鞭を取られた藤原先生の教科書は、
別の力学A/Bの講義でも
採用されている。わたしも物理部会の先生方からこの本を勧められた。
この本は、物理教育、そして物理に熱い思いを抱く藤原先生の気持ちで満ちていて、
自分で全部確かめてやろう、という「熱血」が素晴らしい。特に、剛体の運動の
様子を、ストロボ撮影に収めた写真は、駒場の物理教育のスピリットそのものである。
手を動かし、頭を動かしていくうちに、
物理的な考え方、方法論をものにしていく、という姿勢を学びとるのが、
この本の読み方だろう。
一度、高速で通読し、内容を大雑把に確認してから、
他の教科書で細部を確認する、という読み方でもいいだろう。
数学は、必要になった章で必要なだけ提示されるので、どの物理の内容が、
どの数学技術と関連しているか分かり易い。一方で、うろ覚えの内容を
確認するために見返す際は、ちょっと不便、と感じるかもしれない。
「力学I --質点、剛体の力学--」原島鮮著 (裳華房)
[Hr73]
日本の大学で標準的に採用されている力学の教科書。
推測するに、著者の原島先生は、数値計算による物理研究の先達のひとりではないか。
当時の最先端の「電子計算機」で計算した「地球を回る人工衛星の立体図」の美しさは
、「物理界のモナリザ」と呼んでもよいのではないだろうか?
計算の途中経過が詳細に書かれていて自習に向く。が、細かく書かれ過ぎていて、
それを追っていくうちに、なにがそもそもの目的だったのか忘れてしまいがちに。
たとえば、座標変換の議論はちょっと長過ぎて、なかなか物理に到達しないため、
イライラする人も多いのでは?
ただ、実際に人工衛星の軌道計算など、数値計算をやりはじめるようになれば、
重宝するのかもしれない。数学は、必要最小限を、なるべく易しく書こう、という
立場なので、物理数学の習得には不向き。
「古典力学」スレーター、フランク著、柿内訳(丸善)
[Ko47]
丸善のものは絶版となってしまった。古本やamazonの中古で手に入れるしかない。
が、原著はカリフォルニア大学の蔵書がスキャンされて、
全文がネットで公開されている。
力学Aで習う内容は、第3章までにコンパクトにまとめられている。
必要最小限の内容がスマートに書かれている。
コンピュータが発展する前に書かれた古い教科書なので、
題材が古く、例が少ない(現代では、銀河などの多体力学系や、
カオス力学に基づくシミュレーションなど、
古典物理が「最先端」の研究テーマになることもあり得る)。
が、力学理論における数学的基本構造にだけ着目すれば、
これで十分かもしれない。個人的には、非保存力を数式で扱った(4.1)が一番
気に入っている。この式が出ている教科書は他に見たことがない。
"Classical Mechanics (Third Edition)",
H. Goldstein
(Addison Wesley) [Go02]
アメリカ合衆国の大学院で広く採用されている、古典力学(解析力学)の標準教科書。
古典力学の教科書の「最高峰」といってもよいかも。ただし、この本から
力学を学び始めることはお勧めしない。初学者はあくまで参考書として
使用すべきだが、読めるところもある。剛体の運動方程式であるオイラー方程式を
扱った章は、力学Aで使う。とくに、軸対称性がある剛体の歳差運動の解析では、
調和振動子が出てくるので、力学Aの範囲とみなせる。
21世紀になって、カオス力学が入った改訂版が出た。
「古典力学の形成 --ニュートンからラグランジュへ--」
山本義隆著(日本評論社)[Ya97]
「ニュートン」力学と呼ばれているわりには、この力学はニュートンが
書き上げたものではない。ニュートン力学はライプニッツやオイラーが
微分や積分などの解析学によって展開した力学理論であり、後に
ラグランジュやハミルトンによって解析力学へと進化した物理理論である。
この辺りの力学理論発展の歴史は、ながらく謎であり、
よくまとめられたものがなかったのだが、山本義隆氏によって明らかにされた。
"Philosophiae Naturalis Principia Mathematica",
I. Newton
(Addison Wesley) [Nw46]
1687年に出版された原著はラテン語で書かれており、
そのまま読める人はほとんどいないだろう。ただ、
1846年に英訳されたものがネットで公開されており、
それを読むことができる。ニュートン本人による「力学」理論は
この本で展開され、力学の礎を築いた。が、そこで用いられたのは、
ユークリッド幾何学風の図形的証明であり、微積分を駆使した形式は
採用されていない。微積分の始祖であるニュートンがなぜ、プリンキピアで
それを使わなかったに関しては、科学史家の説明を参考にしてもらいたい。
この本で一番面白いのは、冒頭にある"Definitions"である。
有名なニュートンの3つの法則はここに書かれている。
ニュートン本人が、「運動量」や「慣性」そして「力と運動(加速度)」を
どのように捉えていたか知ることができ、現代の教科書ではさっと通り過ぎてしまう、
これらの概念の深い理解に触ることができる。
以下の文章では、上記の教科書/参考書を引用するとき、本の題名の最後に付した記号、
例えば砂川先生の教科書は[Su77]、を用いることにする。
力学を担当して今年で3年目となる。
1年目は、行列に馴染むために回転や回転系に焦点をあてて講義をした。
2年目は、近似に焦点をあて、テイラー級数展開を中心に、
力学理論の適用範囲に着目しながら講義をした。
3年目の今年は、数学と物理の関連性に着目しつつ講義を組み立ててみたい。
高校で習った「単振動の問題」は、大学の物理では「調和振動子の問題」という。
(ちなみに、英語では、"Simple Harmonic Oscillator"という。
直訳すると「単純調和振動子」となるが、長ったらしいので、
誰かがどちらかを省略したのであろう。)
講義でやったように、次元解析により、バネ定数kは[質量/時間2]の
次元を持つので、k=mω2と置き換えることができる。ωは振動周波数であり、
周期TとはT=2π/ωの関係がある。
講義が終わったあと、「ωではなく、Tを直接使ったらどうなのか?」
というなかなか面白い質問があったので、この場で分析しておくことにする。
たしかに次元解析に従えば、k=m/T2でもよい。
運動方程式は (d2/dt2)x(t) = -(1/T)2 x(t)
となるから、解はx(t)=c1cos(t/T) + c2sin(t/T)となって、
これは数学的にはなんの問題もない、正しい答えである。
しかし、(物理における調和振動の)周期とはx(t+T)=x(t)を満たす時間Tのことである。
上記のTはこれを満たさない。周期の条件を満たすのはT'=2πTである。
たとえば、x(t+2πT)=cos( (t+2πT)/T ) = cos(t/T + 2π)
= cos(t/T)cos(2π) - sin(t/T)sin(2π) = cos(t/T) = x(t)である。
そこで、Tの代わりにT'を用いると、T=T'/2πなので、たとえば、
cos(t/T)=cos(2πt/T')となるが、2π/T'=ωなので、結局cos(ωt)
となってしまうのである。つまり、周期Tではなく、ωを使う理由は、
物理側からの要請であり、調和振動の「周期」の物理的な意味合いを保持するためである。
(数学の側でも「三角関数は周期2πの周期関数だから」という要請があるかもしれないから、
とくに「物理の要請」とは言い切れないのかもしれないが....)
前回の講義終了後、「ωではなくTを用いるのはどうか?」という質問があり、
今回の講義の始めに、上述のことがらをもとに回答した。その際、
ωではなく、Tを用いた方が自然な微分方程式もあることについて言及した。
物理学者が思い描く、ωではなくTが自然になる微分方程式
とは m dx(t)/dt = -kx(t)である。左辺が1階微分になっているが、調和振動子の
微分方程式によく似ている。このときk=m/Tとおくと、この微分方程式の解は
x(t) = x(0)exp(-t/T)となる。
ただし、解の形を見ればわかるように、
このTは「周期」の意味は持たない。講義中に議論したように、
むしろ核物理における「半減期」に近い。(核物理の場合はx(t)の代わりに、
放射性元素の数N(t)とする。)しかし、この微分方程式は「運動方程式」の
形にはなっておらず、力学の問題としては一見無関係に見える。
実は、この微分方程式両辺をもう一度微分すると、
d2x(t)/dt2 = -(1/T)dx(t)/dt
となって、運動方程式(を質量mで割ったもの)にすることができる。
方程式の右辺には負符号があるから、速度に比例して増大する「抵抗力」と解釈できる。
(現実には、低速で移動する場合の空気抵抗、あるいは摩擦力に相当するらしい。
テイラー展開の1次近似だと考えれば、妥当な条件だろう。)
通常の力学の教科書では1/T = γと表記されることが多いが、これがなぜ「半減期」
と同じような意味合いをもっているかは、この段階ではまだ明らかではない。
今週は、ここで一つ面白い質問があった。「いくら自分の望み通りの解が得られたとしても、
x(t)=x(0)exp(-t/T)という形には、積分定数が一つ足りないのではないか?」という
疑問であった。結論からいうと、この疑念はもっともであり、この解では不十分である。
講義直後であり、きちんとした答えができなかったので、ここで議論する
ことにしたい。
自然な物理量としてTを使えるように、という理由で一階の微分方程式をひねくり出した
x(t)=x(0)exp(-t/T)であるが、これは確かに「ひねくり方程式」の両辺を時間微分して
仕立て上げた運動方程式
d2x(t)/dt2 = -(1/T)dx(t)/dt
の解にはなっている。しかし、本来2階であるのだから、未定係数は2つなければならない
はずだ。「ひねくり方程式」の解にはx(0)の一つしかないから、なにかがおかしい、
と感じた件の学生の洞察は正しい。実際、仕立て上げた運動方程式を積分してみると、
x(t) = Tv(0)[ 1 - exp(-t/T) ] + x(0),
v(t) = v(0)exp(-t/T)
となり、未定係数は2つ発生する。上の解は「ひねくり方程式」の解x(t)=x(0)exp(-t/T)
と違う形になっているものの、
x(0)=-Tv(0)とおくと一致することが確認できる。つまり、「ひねくり方程式」の解は
2つの初期条件の間に拘束条件がついた特別な場合に相当している。
微分方程式の自由度の観点からみれば、これはすごく当然のことであるが、
自由度の物理的な意味を考える上で、pedagogicalなケースと言えよう。
さて、今週の宿題は、「T=1/γが半減期と似たような物理的意味をもつかどうか調べよ」
であるが、どうやってそれを調べたらよいだろうか?
それには、微分方程式の初期条件としてx(0)=x0, v(0)=-v0
< 0
としてみるのがよい。これは宇宙ステーション内で、慣性の法則に従って
ゆっくり進んでいたビー玉が、突如、空間に浮いた巨大な水玉に突入するような状況に
相当する。
水玉に突入する瞬間をt=0, 突入速度を-v0,
水玉の中心から表面までの距離をx0
とみなす。
上の2つの式に、この初期条件を代入すると
x(t) = Tv0[ exp(-t/T) - 1 ] + x0,
v(t) = -v0exp(-t/T)
となる。放射性元素の半減期が現れた表式に似ているのは、x(t)よりもv(t)である。
形式的な半減期T
1/2はT
1/2=ln(2) Tで与えられるが、
これが物理的に何を表すかというと、水球内における抵抗力による速度低下が、
初速|v
0|の半分になるまでの時間であり、いわば「速度半減時間」と呼ばれる
べき量である。面白いのは、T→∞の場合のx(t)の収束値であり、
x(t)→x
0 - Tv
0という形で与えられる。
水球の中心から表面までの距離がx
0であるから、Tv
0
は「侵入距離」に相当する。この侵入距離は、初速のまま速度半減時間だけ移動した
等速運動の距離に相当している。実際には、速度を変えながら「複雑な」運動を経て、
侵入距離に到達するわけだが、速度半減時間と初速を用いた等速運動としての「有効理論」
を用いて、現象を直感的に理解することが可能となる。
余力のある学生は、Ginzburg-Landau理論による、超伝導体に侵入する磁場の「侵入長」
の議論と比較してみたらどうだろうか?半減時間や侵入長など、次元解析によって
つくった典型的な物理量を導入することで、
研究対象の物理系を次第に特徴付けしていくのは、
現象論とよばれる物理の方法論におけるオーソドックスな手法の一つである。
また、それは、その後の直感的な議論に役立つことがわかるだろう。
代数的手法は、運動方程式の解x(t)の数学的な形を予想することから始まる(この予想解の
ことをドイツ語でAnsatzという。英語でも科学関係の脈絡なら通じる)。が、
講義でも質問が出たように、いつでもうまい具合に適切な予想ができるとは限らない。
この手法がうまくいくためには、「運」も必要になる。とはいえ、いままでの先人たちの
努力により、「うまく行く」典型的な場合が幾つか知られており、これに習熟するうちに、
新たなAnsatzにたどりつくこともあるだろう。
それはともかくとして、「よく知られている典型例」
のひとつが、今回扱った減衰調和振動子の微分方程式であり、
x(t)=A0exp(λt)というAnsatzが適用できる。
Ansatzを代入すると, 運動方程式はλ2+2γλ+ω2=0
というλに関しての2次方程式に変わる。これを解けば、当然2つの解が得られる。
それをλ+とλ-と表すことにすれば、運動方程式の解は
x(t)=A0exp(λ+t),あるいは
x(t)=A0exp(λ-t)となる。
講義では、この後「ということで、一般解は
x(t)=A+exp(λ+t)+A-exp(λ-t)
となります」と説明したが、これに対して質問が出た:「なぜ線形結合をとるのでしょうか?
片方ずつ選んで、この場合もあれば、あの場合もある、というのではいけないのでしょうか?」
講義中にはとっさに「個別の場合ももちろん解ですが、それは特別な場合にすぎません。
一般解を考えるためには、線形結合をとる必要があります」と答えたものの、
「では、最初のAnsatzの形式が間違っていた、ということなのでしょうか?」と切り返され、
その質問に解する回答は不十分なものしか思いつかなかった。後で考えてみると、この質問は、
線形微分方程式の線形性と関連していることが判明。とてもよい質問なので、
下の文書でちょっとだけ丁寧に説明してみたい。
質問に対する回答の詳細(宿題の解答も最後にある)
Feynman Ch. 25の間違いに関して大賀君が提出してくれたレポートは素晴らしい内容でした。
いくつか、面白い指摘がありましたので、ここで説明しておきます。
- 「固有振動数」が教科書で定義されていないが、これはω0を指すのか、
それともωγ=(ω02-γ2)1/2を指すのか?
「固有振動数」と書くと専門用語のニュアンスが出てしまうが、原著を読むと
"the natural frequency of the oscillator"とある。「固有振動数」というのは、
ちょっと訳者の訳しすぎなのかもしれない。
「自然な」訳をしてみると、「振動子の自然な周波数」となるだろう。
物理では、「自然な」という用語はよく出てくる。これは「無理のない」とか、
「考えると自然に出てくる」とか、「まず最初に思いつくのは」という意味で使われる。
調和振動子はそもそも「振動子」なのだから、振動数ω0で特徴付けられている。
したがって、調和振動子が関わる問題において、「自然な周波数」といえば、
ω0が意味されるのが「自然」であろう。
- 図25-5の共鳴曲線はω0に対して、左右対称にはならないはずであるから、
これが「誤り」ではないか?
この主張は正解であり、また非正解でもある。まずは前者の論拠からいうと、実際
フルの共鳴曲線を数値的に描いてみると「非対称」になる。大賀君が指摘するように、
他の教科書ではこの非対称なグラフがキチンと描かれている。
にもかかわらず、ファインマンの図25-5は左右対称のグラフとなっている。
たしかに、これはファインマンの方が分が悪そうである。次に後者の観点から
見てみると、左右非対称な曲線を与える関係式は、実際にはいわゆる共鳴曲線とは
違う関数系に従っている。確かに、共鳴ピークがそそり立つ図形にはなるが、
左右非対称性が「強すぎる」! 通常の(例えばBreit-Wignerタイプの)共鳴はLorentzian型
の関数で表され、左右対称になる。ファインマンは、ω0〜ωの場合の
共鳴を与える近似式がLorentzianになることを本文で述べているから、図25-5は
このような共鳴周波数付近での近似的な振る舞いを表したものだ、と主張すれば
図25-5は誤りとはいえない。
今回の課題「ファインマンVol.I25章の間違い探し」ですが、この間違いは最近和訳版を
読んでいた時に私自身で気づきました。
実は「ファインマン物理」は印刷ミスが非常に多いことで有名なようです。
これは今回調べて見て初めて知りました。驚きです。最新版のファインマン物理の原著(2011年の
"The New Millennium Edition")は、
長年指摘されてきた誤りの全てを修正したものらしいので、これからファインマン物理を
読んでみようと思っている人は、ぜひこの最新版で勉強するのがよいでしょう。
一方で、間違い探しは、実力向上に役立ちますので、
和訳本を使ってトレーニングするのもよいでしょう。
岩波の和訳版は当分改定されないでしょうから(現に書籍部にあったファインマン物理は
いまだに古い間違いが載っています)、今回の課題以外の「間違い探し」にチャレンジして
みてはどうでしょうか?
次に、damped harmonic oscillatorのグリーン関数を与える方程式は解けるのか?という
質問が講義中にありました。それに対する回答は「解ける」です。x(t)をフーリエ変換したx(k)に
よって、グリーン関数の方程式を書き直すことで、グリーン関数は簡単に積分形で
求まります。この積分をやり抜くと三角関数になるようです。
詳細が気になる方はこちらのノートを参照してみてください。
今回もよい質問が出ました。
「(1次元問題で)ポテンシャルが導入できないような非保存力にはどんなものがあるか?」
という質問です。補足すると、質問者は速度に依存する力は保存力とはならないことは
理解しており、力がF(x)と書けるにもかかわらず、ポテンシャルによってかけない力はあるのか、
ないのか、という質問です。
実は1次元の場合、たいていの連続関数はポテンシャルで書けると思います
(証明はしてませんが)。したがって、ポテンシャルでかけない力F(x)を見つけるとなると、
それは不連続な関数にするとか、通常の力学では扱わないような「不自然な」力に
なっているだろうと思われます。
実は、1次元の力学で導入される「ポテンシャル」は、3次元の力学の「類推」に過ぎず、
必然性をもって導入されたものとは言い切れないところがあります。ポテンシャルで書けない、
位置(x,y,z)だけに依存する力は簡単に見つけることができます。それは、3次元の力学を
議論する際に学習することになりますので、それまでお楽しみに待っていてください。
もう一つの質問は、「非調和振動子のポテンシャルに見られるように、
ポテンシャルエネルギーUが、全エネルギーEを上回るような領域が発生したとき、
そこでは何が起きているか?」というものでした。U=Eとなる場所を「古典的転回点」と
いいます。そこで、質点は向きを変えて反転(転回)するからです。古典的転回点より
向こうにいってしまうと(U>E)、エネルギーの保存則より運動エネルギーは負値となりますが、
運動エネルギーは速度の自乗ですから、v2<0となって、
速度が虚数になってしまいます。この状態は、古典力学では「非物理的な状態」となるので、
除外して考えます。しかし、量子力学ではこのような状態に相当する場所でも波動関数は
定義されます。古典的には禁止される領域を通って、粒子がポテンシャル障壁の外側に
抜け出す現象のことを「トンネル効果」といいます。江崎ダイオードは、トンネル効果を
利用した最初のデバイスの発明ということで、発明者の江崎玲央奈にはノーベル物理学賞が授与
されました。
最近のフラッシュメモリーなどの半導体メモリーも、FNトンネリングというトンネル効果を利用したデバイスです。また、原子核のα崩壊は、核力とクーロンポテンシャルを合わせた有効ポテンシャルに閉じ込められたα粒子がトンネル効果で抜け出す現象としてみなすこともできます。
今回の質問は、「向心力」は振り子の問題でどう扱われるのか?というものでした。
同じ質問が2人から出たので、きっと多くの人が同じ疑問をもったものと思われます。
実は、この問題は「座標変換」のところで取り扱う予定の内容です。コリオリ力や
遠心力なども、そこで議論されます。簡単に言うと、慣性系から観測する場合と、
非慣性系から観測する場合で違いが現れる、ということです。向心力は回転座標系(非慣性系)
にいる観測者だけが感じる「みかけの力」であり、慣性系から観測する人がみれば「向心力はなく、
単なる加速度」として見えます。詳細に関しては、講義の中で再度議論します。
二次元調和振動子のポテンシャルは一般的には
V = (1/2)m(ω2xx2+ω2yx2)
とかける。
対応する運動方程式はxとyに変数分離できるので、1次元の調和振動子を2つ解くような
形になる。その2つの解を合成した2次元曲線は一般に「リサジュー」と呼ばれる曲線となる。
周波数の比が有理数のとき閉曲線となる。ポストスクリプトを使うと、綺麗なリサジューが
かけるのでぜひ試してみてもらいたい。(emacsでもviでもよいので、手頃なエディターで
リサジューを描くプログラムをpostscriptで書いて, lissajous.psという名前で保存する。
これを開くと、MacOSの場合は自動的にpdfに変換され、図形が描画される。
postscriptがどんなものか知らない人は、
こちらのサンプルプログラムを参照のこと。
ダウンロードしたファイルをクリックすると図形が表示されてしまうので、プログラムの内容を
みたければ、openするアプリをエディターに指定して開く必要がある。)
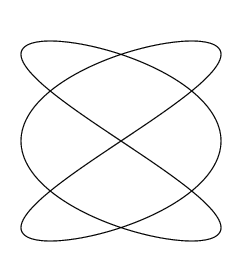
ωx: ωy = 3:2の場合のリサジュー図形
ニュートンのプリンキピアの原文(ラテン語,1765年出版)[
Nw46]は
デジタルアーカイブで閲覧することができる。
冒頭の「公理や運動の法則」(Axiomata, sive leges motus)の部分に、
3つの運動の法則が書かれている。今回の講義で取り上げたのは、最初のコメントで
取り上げられている「慣性の法則」である。
I.
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum,
nisi quatenus illud a viribus impressis cogitur statum suum mutare.
ラテン語の翻訳はtranslate.google.com
で可能であるが、
Motteによる1846年の英訳の方が信頼できるだろう。
I.
Every body preserves in its state of rest, or of uniform motion in a right line,
unless it is compelled to change that state by forces impressed thereon.
これを訳してみたのが、下の文である。
壱.
物体は, その状態が力によって変化させられない限り, 静止の状態, あるいは直線に沿った
均一の運動, をとり続ける。
今回の宿題は、山本義隆[Ya97]で議論されている「順問題」である。
すなわち、与えられた軌道を実現するのに必要な力はどのような形式で書かれるべきか、
という問題である。ケプラー問題の場合は、楕円軌道を形成する重力とは、いったいどのような
形式で書かれるべきか、という「順問題」であった(答えは逆二乗則)。(ちなみに、
「逆問題」に相当するのが、ほとんどの現代の力学教科書に書かれている、逆二乗則から
楕円軌道を導く問題である。)
- 等速円運動を実現する力はどのような数学的表現になるか、順問題を解け。
- 非等速円運動を実現する力はどのような数学的表現となるか、順問題を解け。
問1の答えとして、高校の物理で習ったタイプの向心力が出てくる。
ちなみに、等速円運動は、アリストテレス学派(特にエウドクソス)が天体の運動に対して
導入した考え方(天動説)としてよく知られる。また、天動説の完成形である、プトレマイオスの
天動説(アルマゲスト)では「エカント」の概念が導入されたが、
これは実質的に「非等速円運動」を認めたものと解釈できる。問2では、角速度ωが時間の関数と
なることを確認してもらいたい。古代天文学に興味のある人は、エカントを実現するような
ω(t)を導入して、その軌道がどのようななるか研究してみてもよいだろう。このあたりの
研究は、藤原先生の教科書[Fj84]でも展開されているので、参考にしてみたらよいだろう。
山本[Ya97]で紹介されている「順問題」に関しての質問(複数)、
および2次形式の対角化についての質問(複数)がありました。
数学的な側面からみると、この2つの質問は随分違うことに関することのように感じがしますが、
要はどちらも「楕円」に関するものです。
まずは2次形式で表される楕円の方程式から。a,b,cを実定数(a, cは非零)とすると,
デカルト座標(x,y)において楕円の方程式は
ax2 + 2bxy + cy2 + d =0
と2次形式で表すことができる。行列を用いると

となる。行列をAで表せば、Aは実対称行列であり(A
T=A)、
常に対角化をすることができる(線形代数の定理による)。言い換えれば、
Aが対角行列で表されるような新しいデカルト座標系(x',y')を
見つける操作が、この問題における「対角化」の意味となる。
最初の座標系(x,y)と
新しい座標系(x',y')を結びつける線形変換をUとする。このUは実直交行列であり
(UTU=UUT=I)、
回転と鏡映反転の組み合わせで表すことができる。実直交行列の行列式は
{det(U)}2=1であり、回転行列の行列式は+1、鏡映反転行列の行列式は-1となる。
Uの表現に関する詳細な議論は, こちらのノートを参照
のこと。
[問題] 角度θだけ傾いた楕円をpostscriptで描画する方法を考えよ。
次は、2次元調和振動子のデカルト座標を用いた解(等方解ωx=ωy)は
x(t) = Axcos(ωt+δx)
y(t) = Aycos(ωt+δy)
であり, 加法定理と三角関数の性質を利用してtを消去することができる。その結果、
2次元調和振動子の軌跡は2次形式、すなわち楕円で表せることは講義中に証明した。
その際、計算を簡単にするため振幅の大きさをxとy方向で同じ大きさ(A
x=A
y=1)にした。2次形式を対角化した結果, xおよびy軸方向の楕円の軸半径はそれぞれ
(√2)sin(Δ/2), (√2)cos(Δ/2)となる。
ただしΔ=δ
x-δ
yである。
ここで宿題「振幅が共通なのに軌道は円とならず楕円となるのはどうしてか?」を出題した。
もちろん、軌跡が円になるときもあり、それは位相差Δ=π/4 (mod 2π)の時である。
また、Δ=0 (mod 2π)の場合は、軌跡は線分に潰れる。
しかし、その他の場合は楕円となる。これはリサジュー図形のしくみを思い出すとわかりやすい。
つまり、各自由度(x,yのこと)が最大値をとる時間(振幅一杯に振れる時間)が、位相差によって
ずれているのが楕円となる理由である。詳しくは、自分で図を描いて分析してみよう。
2次元調和振動子の解が楕円であることが確認できた後に、次の宿題を出した。
「ケプラーの法則では、惑星の軌道が楕円であると述べている。「順問題」を解くことによって
ニュートンは天体間の作用/力が逆二乗則に従うことを導き出した。では、同じ楕円軌道
を与える2次元調和振動子という誤答に迷い込まなかったのはどうしてか?」
この問題に関して複数の質問/意見が寄せられたが、それに対する回答は重力理論を講義で
説明してからにしたい。
今回の宿題:動径座標r(t)をansatz法にて求め、それが三角関数であることを確認せよ。
r(t) = (x(t)2 + y(t)2)1/2であることから
デカルト座標で求めた解を代入してr(t)のansatzを求めることができる。
これはCaltechのDr. Golwalaが採用した手法(p.164の"Isotropic two-dimensional harmonic oscillator"を参照)。簡単のためx(t)=cos(ωt+δ), y(t)=cos(ωt)で計算してみること。
(注:Golwalaの原文ではcosの代わりにsinが採用されている。)
今回の講義では、GolwalaのようなAnsatz法ではなく、Goldsteinにあるような
エネルギー積分を経由する「正統的な積分」による解法について解説した。
V=arn+1タイプのポテンシャルでかける中心力は、
n=1, -2, -3の場合は三角関数として、n=5,3,0,-4,-5,-7の場合は楕円関数として
積分可能であるらしい。今回の講義ではn=1の場合をやった。n=-2の場合は
重力のところで取り上げる。その他の場合は(特に楕円関数となる場合)講義で取り上げないので
「夏休みの自由研究」としてチャレンジしてみたらどうだろうか?
数値計算をしてみてもよいだろう。
(それらの結果はぜひレポートしてもらいたいと思います。)
n=1の場合(実はn=-2の場合も), dr/dtを(dr/dθ)(dθ/dt)と書き換え、2つ目の微分因子は
角運動量の法則を使ってr2依存する因子で書き直した。
この後、u=1/rと変数変換するという「作法」がGoldsteinには書いてあるが、n=1の場合は
この変数変換の結果は、講義で私が偶然やってしまった結果と同じ結果となる。
つまり、この書き換えはn=1の場合は不要で、そのままdr/dtの積分を実行することが可能だ。
その詳しい内容および2次元調和振動子の「駒場解」は、
こちらのノートを参照されたい。
さて、前回の宿題は、デカルト座標で解いた(等方的な)2次元調和振動子の解から
tを消去して、xとyの関係が楕円となることを示せ、というものだった。
これに対して3人からレポートがあったが、
どれも素晴らしい出来栄えだった。(各レポートに対するコメントはこちらのノートを参照。)
この宿題では、対角化の手法の習熟、2次形式の標準化の幾何学的な意味(回転と反転)などを
学習することができるので、まだやってない人はぜひ挑戦してもらいたい。計算が大変なので、
途中で計算ミスが入り込むのは仕方のないことである。しかし、その間違いは、次元解析や
物理的、幾何学的な考察をすることで、無くしていくことが可能である。
その「デバッグ」の技の習得も含めて、頑張って計算してみる価値はあるだろう。
(私のように)途中で投げ出して、簡単な近似計算や特別な例に逃げてもいいだろう。
大事なのは、計算するだけではなくて、得られた解を物理的に吟味することだ。
講義では、Ax=Ay=1$という特別な場合
を考察し(逃げ)たが、振幅が等しいのにも関わらず軌跡は楕円になる理由について考察してみると
おもしろいと思う(位相のずれと密接な関係がある)。この考察の延長上には、
リサジュー図形がなぜあんな形になるのか理解する鍵があると思われる。
ところで、今回提出してもらったレポートはすべて手書きで仕上げられていたが、
数式を含んだ文書作成は、将来的には論文作成へと進展していくことになるので、LaTeXを用いた
レポート作成を今のうちから練習しておいてもよいだろう。たとえば、
こちら(理学部三年生向けの計算機実験の講義ノート)を参考にして、
大学の情報センターなどのシステムを利用してLaTeXで数学/物理の文書を作成してみよう。
講義の最後に出た質問で「ケプラーが楕円軌道に気づいたのは、重力の形式が逆二乗則に
なることを薄々感じていたからか?」というものがありましたが、とても面白い質問です。
これに対する答えは、講義中にも答えましたが、そのネタ本は
アーサーケストラー著「ヨハネスケプラー ー近代宇宙観の夜明けー」
ちくま学芸文庫(2008)。
です。一読の価値があります(原著はドイツ語だと思います)。
また、ケプラーによるティコブラーエ暗殺の疑いに関する本に、
ギルダー著「ケプラー疑惑」地人書館(2006)があります。なかなか面白い話だと
思いますが、最近この「疑惑」は晴れたようです。
今回の講義では, ケプラーの法則を数式で表すこと、
およびそこから順問題を解いて逆二乗則を導出すること、などを取り上げた。
戸田[Td82]の教科書を参考にして、
ケプラーの第1と第2法則は逆二乗則に対応しており、第3法則は「万有」であることを示す
ために必要であることをみた。
講義では、a3/T2 =K(一定)という
ケプラーの法則をa/T2 = K/a2と書き換え、次元解析から
左辺は加速度に対応する。したがって、両辺に質量をかければ運動方程式と
同じ関係になることからK=GMと置いた。
これに関して質問がでたが、あくまで次元解析なので、これ以外の
表現も可能だろうし、だいたい比例係数は次元解析では合わせきれない(最後に
G'=4π2Gという「くりこみ」が必要になったのは、このせい)。
K=GMという組み合わせは、あくまで我々がすでに答えを知っているからというのもあるし、
「今考えている流れではもっとも自然なチョイスだから」というふうにも説明できるだろう。
ケプラーのオリジナルの文書には、Gも出てこないし、太陽の質量Mも出てこない(
"Harmonices Mundi", 翻訳「宇宙の調和」, の第5巻第3章命題8)。
Gを最初に測ったのはキャベンディッシュ(1798年)であり、太陽の質量を最初に推定したのは
(Wikipediaによると)ニュートンだというから、いずれにせよ、ケプラーよりも後の話である。
ケプラーの第三法則を記述したオリジナルの文
("Harmonices Mundi", Vol. 5, Chap.3, Th.8, [1619]) は次のとおり。
Sed res est certissima exactissimaque, quod proportio quae est inter binorum
quorumconque planetarum tempora periodica, sit praecise sesquialtera proportionis
mediarum, id est orbium ipsorum.
次に、ケプラー第二法則(面積速度一定)の幾何学的な考察をしたが、
余弦定理の適用のところでちょっとへんなことになってしまった。
あとで考えてみたら、テイラー展開の近似の次数が他の近似と調和してなかったのが
原因であった。詳細に興味がある人はこちらのノート
を参照してもらいたい。
また、r(t)は時間の関数なのに、なぜ微分はδr/δtだけを考えるのか?という質問もあった。
r(t+δt)=r(t) + δrなので、微分の定義によればr(t+δt)-r(t) =δrとなるから、と言ってしまえば
それまでだが、たぶんこの認識の先に目を向けた疑問だったと感じた。
δtの間に変化するのはδrだから、この微小時間内における力学変数として意味を持つのは、
r(t)よりもδrであろう。むしろr(t)はδtの間は「凍りついていて」定数のようにみなせる。
0〜tという時間間隔においてはr(t)は当然ながら力学変数である。しかし、δtという短い時間では
δrの方が力学変数の自由度を担っているといえる。これが微分の物理/力学的解釈の
本質なのではないだろうか?こういう考え方は、熱力学でも登場する。
断熱変化が一番近いだろうか?ある物理量の変化にくらべ、別の物理量がものすごい速く
変化するとき、最初の物理量はほぼ一定(この場合は熱平衡)になっていると考える。
(ただ、そのあとで「高速」変化した物理量の影響が伝わって、
ゆっくり熱力学的な状態は別の平衡状態へと転移する。)
いわば「こいつ見ているな」というDioの感覚である。
宿題:位置ベクトルr(t+Δt)、および速度ベクトルv(t+Δt)
のテイラー展開を行い、そこに中心力に対する運動方程式ma(t) = f(r)r(t)
を適用すると、この運動方程式に従う質点は2次元平面内に閉じ込めらることを示すことができる。
それを示せ。また、この平面と角運動量Lとの関係を確認せよ。
今回もレポートが複数提出された。全てのレポートが優秀な出来であった。
特にケプラー問題において、回転自由度の周期と、動径自由度の
周期が1:1になっていることを議論した、久世くんのレポートは秀逸だった。
藤丸くんは間接的にではあるが、数値計算によって動径の振動周期と、回転の振動周期が
太陽ー地球系の場合に一致していることを確認している。また吉野くんは次元解析により、
得られた解の正当性を確認している。これらの確認は研究者になるためには必須な心構え
であり、それが学部一年の段階で会得されているところを高く評価したい。
講義の後(それから飯島くんのレポートでも)、微分方程式の積分定数についての質問があった。
n階の微分方程式を解くと、積分定数がn個出てくる。これは初期条件や境界条件を別個に与えないと
決まらない定数で、一般解の表式においては「これらは積分定数である」と書き添える「習わし」になっている。たとえば、2次元調和振動子の問題では、2階の微分方程式が2つ出てくるので、積分定数は4つである。特に、デカルト座標で解く場合は振幅Ax, Ayの2つ、
それから位相δx, δyの2つの、合計4つである。
一方、極座標で解く場合には、角運動量保存則と、エネルギー保存則の2つが「積分定数」として
出てくるので、Ansatz法から出発した場合は、(Ax,Ay,δx,δy)のうち、2つまではEとLを使って書き換える必要がある。しかし、最後の2つはそのまま積分定数として残ることになる。(実際、飯島くんのレポートでは、AxとAyを決定する条件式2つが、EとLを用いて得られている。したがって、δx、δyが未定の積分定数となる。)積分定数は、初期条件や境界条件を新たに課してやることで決める(特定する)ことができる。
宿題1:慣性系で等速直線運動する質点を、回転系で観測するとどんな運動になるか調べよ。
宿題2 : 月と地球の重心の位置がどこにくるか概算し、潮の満ち引きが1日に2回発生することを
説明せよ(後半部分はファインマンに解説あり。)
前回の宿題に対するレポートで、中心力にしたがう質点が2次元平面に閉じ込められる説明として、
大枠ではちゃんと説明できていたとおもいます。テイラー展開の2次以降の項が、
運動方程式によって低次(すなわち、位置と速度)の項にくり込めるというのがポイントで、
最後にベクトルの1次独立の性質を述べて証明終わりとなります。
ただし、r(t)とv(t)が1次従属の場合についての議論も一応しておいた方がよい
と思います。今回提出してもらったものには、この点を考察したものはありませんでした。
簡単なので、ぜひやってみてください。
2体問題の応用として系外惑星(Exoplanets)の探索(位置天文学法, Astrometry)
があることを講義で触れました。現在までに確認された系外惑星のNASAによるデータベース
はこちらにあります。
DATA → Confirmed Planet Tableと進むと発見された天体のデータが出てきます。
July 6, 2017現在3498個発見されています。このうち、Discovery Method = Astrometry
と指定して検索して出てくるのはただ一つDENIS-P J082302.1-491201 bです。
これは帆座(南半球でしか見れない星座のようです)に位置する恒星系に属する惑星と考えられています。一方で、ドップラー効果を用いた視線速度法(Radial velocity)で発見されたものの総数を検索すると639個も出てきます。r(t)よりもv(t)の方が現代の科学者には測定しやすいようです。
その理由を考察してみるのもおもしろいでしょう。(ちなみに、日本版のWikiediaでは
AstrometryがStrometryと誤記されていると言いましたが、
それはこちらのことです。)
満潮干潮の問題で、月の軌道の離心率を自分で測定する方法についても簡単に紹介しました。
デジカメを使って、スーパームーンとマイクロムーンを撮影し、gimpなど画像処理ソフトを
使って視直径の比を求めます。ε= (1-k)/(1+ k)、ただしk=θ1/θ2
でθ1がスーパームーンの視直径、
θ2がマイクロムーンの視直径です。
残念ながら、今年のマイクロムーンは先月だったため、
過ぎ去ってしまいました。またスーパームーンは今年は新月で観測するのがよいのですが、
それも6月でした。とはいえ、7月, 8月の満月、新月を利用しても、おおよその値は出ると
思いますから、ぜひチャレンジしてみてください。ちなみに新月の観測は非常に難しいので、
2日月を利用します。地球照が写る程度に露出時間をあげて撮影します。
2016年度Sセメスター(水曜日4限)開講:理科I類(24,25,26組)
f(x)=1/(1-x)のテイラー展開:
テイラー展開(マクローリン展開)の数値計算を行い、その収束性を調べる。
まずはそれぞれの級数展開を書き下し、その収束(絶対収束)領域を計算すると次のようになる。

gnuplotで
3次までの多項式近似したグラフを描くと次のようになる。
図では縦軸がf(x)、横軸がxに対応している。
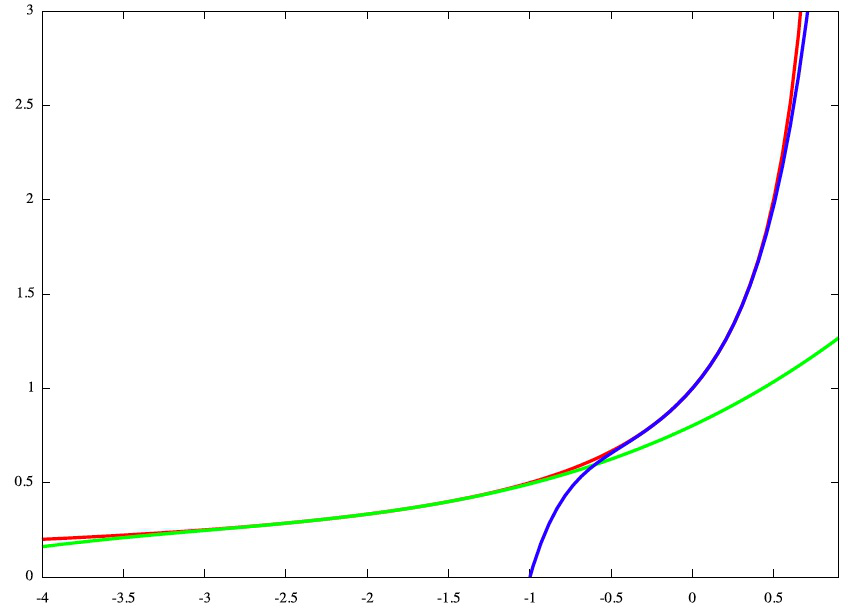
赤線グラフが式(1)、すなわちオリジナルの関数グラフ、青線グラフが式(2)、すなわち
マクローリン展開、緑線グラフが式(3)、すなわちx=-2周りのテイラー展開に対応する。
有限次で打ち切った多項式近似は、展開の中心でよくオリジナルの関数を
近似しているが、そこから外れた場所では近似が著しく悪化しているのがわかる。
しかし、数学的には(2)のグラフは-1<x<1の領域で、(3)のグラフは-5<x<1
の領域で、オリジナルの関数(1)に収束するはずである。上のグラフでそうはみえないのは
打ち切り誤差のせいで、特にそれは(3)に対応する緑線グラフのx> -1の領域で顕著である。
そこで、数値計算を行って、200次の多項式近似を行ってみる事にする。
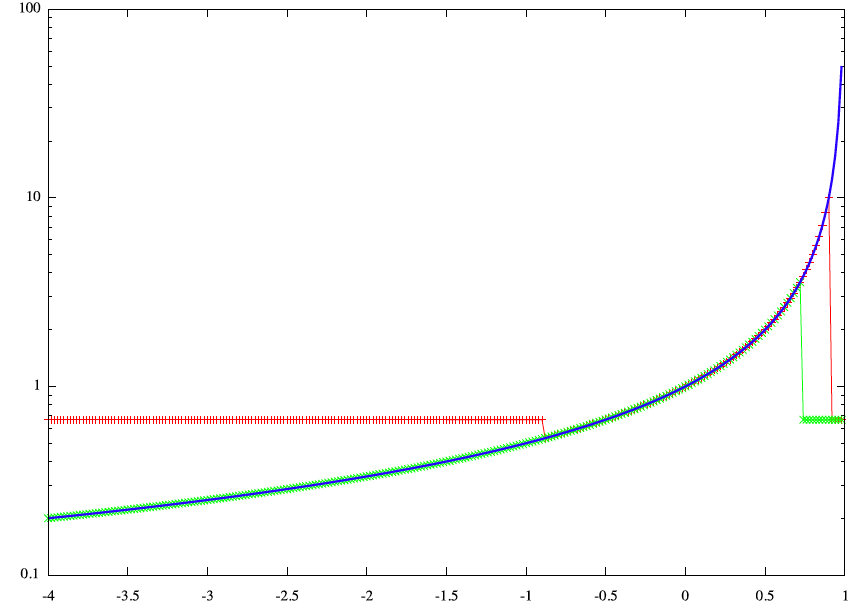
この図では縦軸が対数プロット(logf(x))にしてある。
また、級数の収束が悪い領域ではf(x)=0.666の値を強制的に代入している。
ここまで展開の項数を増やせば、
オリジナルの関数との一致は大幅に改善し、展開の中心から外れても収束が実現されている
のが確認できる。また、共通の収束範囲(-1<x<1)において、
級数(2)と(3)のグラフ、すなわち赤線グラフと緑線グラフの一致も改善している。
数値計算の概要
級数展開を数値計算で確認/研究するときは、無限項の和をとることは不可能なので、
有限項で打ち切る計算をすることになる。
このとき、計算機の限界が許す限り、なるべく高次の項まで
和をとると、より精度の高い計算となる。
通常の関数や初等関数であれば、その冪級数近似は法則性をもった項によって形成される。
特に、n次の項とn+1次の項に関係がある場合、漸化式によって表現できる。ここで計算している
f(x)=1/(1-x)の場合もこれに適合する。式(2)の場合は展開係数c(n)=1と定数、式(3)の場合は
c(n)=3-n-1である。
漸化式をc(n+1)/c(n) = rと置くと、前者の場合はr=1,後者の場合は
r=1/3である。
この結果を用いると、第n項までの和S(n)と第n+1項までの和S(n+1)の間には、
S(n+1) = S(n) + c(n+1) * x
= S(n) + c(n) * r * x
という関係がある。したがって、S(0)とc(0)の値を
初期値として、任意の次数までの有限和を次のようにして計算することができる。
(下のプログラムでは1000次までの計算をすることになっているが、倍精度の精度で
有限和が収束したときは、その時点での次数で計算を切り上げることにしている。
その場合の結果は、1000次までの計算をしたときと変わらないので。)
/* MacLaurin expansion for 1/(1-x) */
#define C0 C_init // value of zero-th term
#define S0 C0 // partial sum upto zero-th order
#define R0 R_val // initial ratio c(1)/c(0)
#define X0 X_val // evaluation point
#define IMAX 1000 // max order for expansion
#define EPS 1.0e-15 // convergence condition (double precision)
int main(void){
double c, s, x, r, s_prev;
c = C0; s = S0; x = X0; r = R0;
for(int i=1; i<= IMAX; ++i){
s_prev = s;
c *= r;
s += (c * x);
if(fabs(s - s_prev) < EPS) break;
}
printf("S("%4d") = "%10.6f,i,s);
return(0);
}
たとえば、x=1/5におけるマクローリン展開を行うと、22項までの展開で
有限和は収束し、その値はS=1.250000000000000となり、実際の値と一致する。
(ちなみに、20項までの和を計算するとS=1.249999999999998となる。)
実際の計算ではC_init=1.0, R_val=1.0, X_val=1./5とおく。
次に、x=aまわりのテイラー展開の数値計算をしてみる。上のプログラムを拡張すると
次のようになる。
/* Taylor expansion for 1/(1-x) */
#define C0 C_init // value of zero-th term
#define S0 C0 // partial sum upto zero-th order
#define R0 R_val // initial ratio c(1)/c(0)
#define A0 A_val // center point of expansion
#define X0 X_val // evaluation point
#define IMAX 1000 // max order for expansion
#define EPS 1.0e-15 // convergence condition (double precision)
int main(void){
double c, s, x, r, s_prev;
c = C0; s = S0; x = X0 - A0; r = R0;
for(int i=1; i<= IMAX; ++i){
s_prev = s;
c *= r;
s += (c * x);
if(fabs(s - s_prev) < EPS) break;
}
printf("S("%4d") = "%10.6f,i,s);
return(0);
}
展開の中心をa=-2に選び、x=1/5における計算を実施すると
第108項で有限和は収束し、S=1.249999999999999を得る。
(C_init=1/3, R_val=1/3, A_val=-2, X_val=1/5とする。)
プログラムを上図のような結果を出力するように変更するには、まずxを走らせるようにし、
次に収束次数を確認する代わりに、展開次数を固定し、その次数までに収束しなければ
強制的にS=0.666と結果をおくようにプログラムを改良すればよい。
(Wikipediaより引用)








